Một khối tròn xoay có dạng như hình vẽ. Các kích thước (tính cùng đơn vị dài) cũng được cho kèm theo. Tính diện tích xung quanh khối tròn xoay đó.
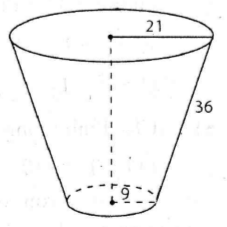
Diện tích xung quanh (mặt nón cụt) cần tìm bằng diện tích xung quanh mặt nón lớn có bán kính đáy \(21\) trù đi diện tích xung quang mặt nón nhỏ có bán kính đáy \(9\). (xem hình vẽ dưới)

Gọi \(l\) là đường sinh của hình nón nhỏ , dựa vào tam giác đồng dạng ta có:
\(\frac{9}{21}=\frac{l}{l+36}\) \(\Rightarrow l=27\)
Suy ra diện tích xung quanh cần tìm là:
\(S_{xq}=\pi.21.\left(l+36\right)-\pi.9.l=\pi\left[12.l+21.36\right]\)
\(=\pi\left[12.27+21.36\right]=\pi\left[12.27+3.7.4.9\right]=\pi.27\left[12+28\right]=27.40.\pi\)
