Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng \(a\sqrt{2}\)
a) Tính diện tích xung quanh, diện tích đáy và thể tích của khối nón tương ứng
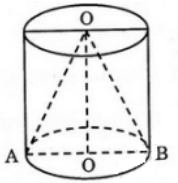
b) Cho dây cung BC của đường tròn đáy hình nón sao cho mặt phẳng (SBC) tạo với mặt phẳng chứa đáy hình nón một góc \(60^0\). Tính diện tích tam giác SBC ?
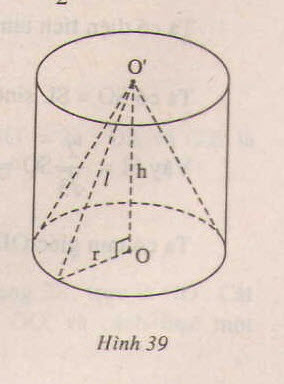



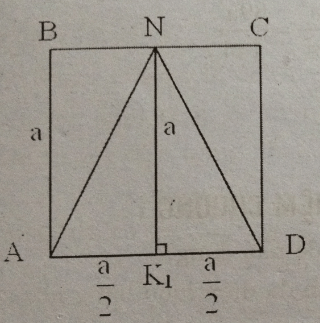

a) Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy r =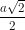 và đường cao h = r, đwòng sinh l = a.
và đường cao h = r, đwòng sinh l = a.
Vậy Sxq = πrl =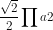 ( đơn vị diện tích)
( đơn vị diện tích)
Sđáy =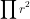 =
= 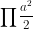 ( đơn vị diện tích);
( đơn vị diện tích);
Vnón =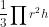
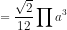 ( đơn vị thể tích)
( đơn vị thể tích)
b) Gọi tâm đáy là O và trung điểm cạnh BC là I.
Theo giả thiết,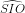 = 600.
= 600.
Ta có diện tích ∆ SBC là: S = (SI.BC)/2
Ta có SO + SI.sin600 =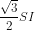 .
.
Vậy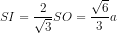 .
.
Ta có ∆ OIB vuông ở I và BO = r =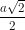 ;
;
OI = SI.cos600 =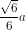 .
.
Vậy BI =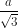 và BC =
và BC = 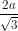 .
.
Do đó S = (SI.BC)/2 =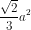 (đơn vị diện tích)
(đơn vị diện tích)
Trả lời bởi Minh Thư