Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mp \(\left(\alpha\right)\) đi qua BD và song song với SA, mp\(\left(\alpha\right)\) cắt SC tại M. Chọn khẳng định đúng.
\(\dfrac{SM}{SC}=\dfrac{1}{2}\).\(\dfrac{SM}{SC}=\dfrac{1}{3}\).\(\dfrac{SM}{SC}=\dfrac{2}{3}\).\(\dfrac{SM}{SC}=\dfrac{1}{4}\).Hướng dẫn giải: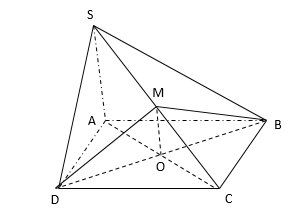
Xét giao tuyến của mp\(\left(\alpha\right)\) với mp(SAC).
Gọi O là giao điểm của AC và BD. Suy ra \(O\in mp\left(\alpha\right)\cap mp\left(SAC\right)\).
Do mp\(\left(\alpha\right)\) // SA nên trong mp(SAC) từ O kẻ đường thẳng song song với SA cắt SAC tại M.
Suy ra \(M\in mp\left(\alpha\right)\cap mp\left(SAC\right)\).
Vậy giao tuyến của mp\(\left(\alpha\right)\) với mp(SAC) là MO.
Có O là trung điểm của AC và MO // SA nên M là trung điểm của SC.
Suy ra \(\dfrac{SM}{SC}=\dfrac{1}{2}\).
