Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều, \(SA\perp mp\left(ABC\right)\). Gọi \(\left(P\right)\) là mặt phẳng qua \(B\) và vuông góc với \(SC\). Thiết diện của \(\left(P\right)\) và hình chóp \(S.ABC\) là
Tam giác đều.Tam giác nhọn.Tam giác vuông.Tứ giác.Hướng dẫn giải: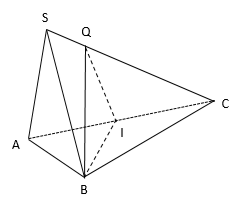
Gọi I là trung điểm của BC. Suy ra \(BI\perp AC\) mà \(SA\perp BI\) nên \(BI\perp mp\left(SAC\right)\).
Suy ra \(BI\perp SC\). Vậy \(I\in mp\left(P\right)\).
Trong mp(SBC) kẻ \(BQ\perp SC\)\(\left(Q\in SC\right)\).
Thiết của mp(P) với hình chóp là tam giác BQI.
Do \(BI\perp mp\left(SAC\right)\) nên \(BI\perp IQ\).
Suy ra tam giác BQI vuông tại I.
