Hỗn số

Ta có một ví dụ về hỗn số. (như ảnh)

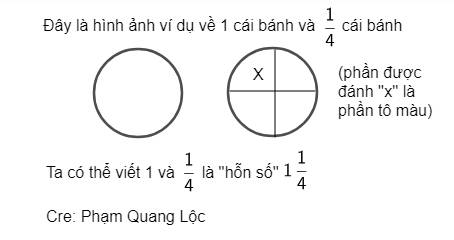
*Hỗn số có hai phần. Phần nguyên và phần phân số.

*Phần phân số của hỗn số bao giờ cũng bé hơn một đơn vị.

*Khi đọc (hoặc viết) hỗn số ta đọc (hoặc viết) phần nguyên rồi đọc (học viết) phần phân số.

Cách đọc: Ta đọc phần nguyên của hỗn số đó trước rồi mới đọc phần phân số.

Ví dụ: \(1\dfrac{1}{4}\) được đọc là ''một và một phần bốn''

Bài tập vận dụng.

Bài 1. Bạn Nam có \(2\) cái bánh. Bạn Lan có \(\dfrac{1}{5}\) cái bánh. Tìm tổng số bánh của cả hai bạn (Viết kết quả dưới dạng hỗn số)

Bài 2. Đọc các hỗn số sau (theo mẫu):

Mẫu: \(10\dfrac{2}{3}\): mười và hai phần ba​​

\(4\dfrac{6}{10}\): ..................................................

\(8\dfrac{2}{15}\): ..................................................

\(3\dfrac{4}{24}\): ..................................................

Bài 3. Viết các hỗn số sau (theo mẫu):

Mẫu: mười hai và bốn phần năm: \(12\dfrac{4}{5}\)

Tám và chín phần mười sáu: ..................................................

Hai và một phần ba: ..................................................

Bốn và mười phần mười ba: ...................................................

Bài 4. So sánh các hỗn số sau:

\(9\dfrac{2}{4}.....3\dfrac{6}{7}\)                    \(6\dfrac{3}{10}.....4\dfrac{5}{6}\)

\(1\dfrac{3}{7}.....3\dfrac{17}{20}\)                  \(7\dfrac{1}{3}.....5\dfrac{9}{11}\)