Bài tập chủ đề 1
Nội dung lý thuyết
Các phiên bản khác1. Trái Đất quay quanh Mặt Trời theo quỹ đạo có bán kính 150 000 000 km.
a. Phải mất bao lâu để ánh sáng đi từ Mặt Trời đến Trái Đất? Biết tốc độ ánh sáng trong không gian là 3,0 x 108 m/s.
b. Tính tốc độ quay quanh Mặt Trời của Trái Đất. Giải thích tại sao đây là tốc độ trung bình, không phải là vận tốc của Trái Đất.
Hướng dẫn:
a. Đổi: 150 000 000 km = 150 000 000 000 m
Thời gian để ánh sáng từ Mặt Trời đến Trái Đất:
\(t = \frac{s}{{\rm{v}}} = \frac{{150000000000}}{{{{3.10}^8}}} = 500\) s \(\simeq8,3\) phút
b. Chu kì quay quanh Mặt Trời của Trái Đất là 365 ngày, ta có:
T = 365 ngày = 31536000 s
Tốc độ quay quanh Mặt Trời của Trái Đất là:
\({{v}} = r.\omega = {150.10^9}.\frac{{2\pi }}{T} = {150.10^9}.\frac{{2\pi }}{{31536000}} = 29885,78\) m/s
Đây là tốc độ trung bình, không phải vận tốc của Trái Đất vì: vận tốc được xác định bằng thương số giữa độ dịch chuyển và khoảng thời gian; khi Trái Đất quay hết một vòng quanh Mặt Trời thì độ dịch chuyển của nó bằng 0, khi đó vận tốc của nó bằng 0.
2. Một người đi bằng thuyền với tốc độ 2,0 m/s về phía Đông. Sau khi đi được 2,2 km, người này lên ô tô đi về phía Bắc trong 15 phút với tốc độ 60 km/h. Bỏ qua thời gian chuyển từ thuyền lên ô tô.
Tìm:
a. Tổng quãng đường đã đi.
b. Độ lớn của độ dịch chuyển tổng hợp.
c. Tổng thời gian đi.
d. Tốc độ trung bình tính bằng m/s.
e. Độ lớn vận tốc trung bình.
Hướng dẫn:
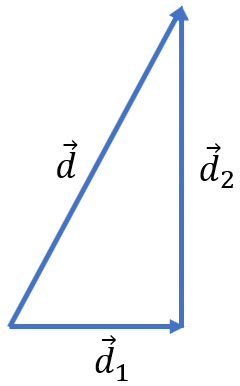
a. Đổi: 2,2 km = 2200 m
15 phút = 900 giây
60 km/h = \(\dfrac{50}{3}\) m/s
Quãng đường người này đã đi về phía Bắc là:
\({s_2} = {{{v}}_2}{t_2} = \frac{{50}}{3}.900 = 15000\) m
Tổng quãng đường đã đi là:
\(s=s_1+s_2=2200+15000=17200\) m
b. Từ hình vẽ, độ lớn của độ dịch chuyển tổng hợp là:
\(d=\sqrt{d_1^2+d_2^2}=\sqrt{s_1^2+s_2^2}=\sqrt{2200^2+15000^2}=15160,5\) m
c. Thời gian người này đi hết quãng đường s1 là:
\({t_1} = \frac{{{s_1}}}{{{{{v}}_1}}} = \frac{{2200}}{2} = 1100\) s
Tổng thời gian người đó đã đi là:
\(t=t_1+t_2=1100+900=2000\) s
d. Tốc độ trung bình trên cả quãng đường đi là:
\({{v}} = \frac{s}{t} = \frac{{17200}}{{2000}} = 8,6\) m/s
e. Độ lớn của vận tốc trung bình:
\(\text{v}=\dfrac{d}{t}=\dfrac{15160,5}{2000}=7,58\) m/s
3. Hai người đi xe đạp theo một con đường thẳng. Tại thời điểm t = 0, người A đang đi với tốc độ không đổi là 3,0 m/s qua chỗ người B đang ngồi trên xe đạp đứng yên. Cũng tại thời điểm đó, người B bắt đầu đuổi theo người A. Tốc độ của người B tăng từ thời điểm t = 0,0 s đến t = 5,0 s, khi đi được 10 m. Sau đó người B tiếp tục đi với tốc độ không đổi là 4 m/s.
a) Vẽ đồ thị độ dịch chuyển – thời gian của người A, từ t = 0,0 s đến t = 12,0 s.
b) Khi nào người B đuổi kịp người A.
c) Người B đi được bao nhiêu mét trong khoảng thời gian đi với tốc độ không đổi (đến khi gặp nhau)?
Hướng dẫn:
a. Độ dịch chuyển của người A được xác định qua công thức:
\(d = vt = 3t\)
Ta có bảng số liệu sau:
| t (s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| d (m) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
Từ đó ta vẽ được đồ thị độ dịch chuyển – thời gian của người A, từ t = 0,0 s đến t = 12,0 s như sau:
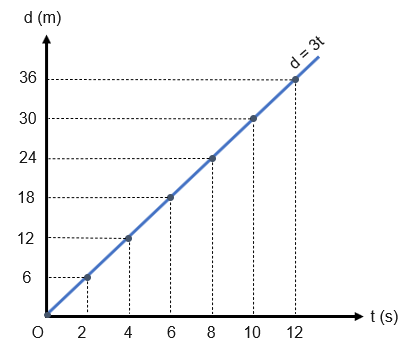
b. Người B trong thời gian từ t1 = 0 s đến t2 = 5 s đi được quãng đường s2 = 10m.
Trong thời gian từ t1 = 0 s đến t2 = 5 s thì người A đi được quãng đường là:
Tính từ thời điểm t = 5 s người B đi với vận tốc không đổi v2 = 4 m/s, người A vẫn đi với vận tốc v1 = 3 m/s.
Giả sử hai người gặp nhau tại vị trí C và tại thời điểm t3. Khi đó ta biểu diễn vị trí của hai người A và B qua sơ đồ như sau:
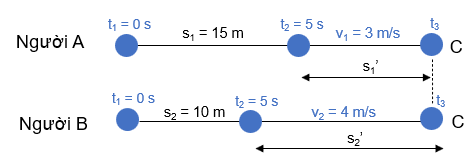
Hai người gặp nhau khi quãng đường họ đi được kể từ thời điểm t1 = 0 s đến thời điểm gặp nhau t3 là bằng nhau, ta có:
\(s_A=s_B\Rightarrow s_1+s_1'=s_2+s_2'\)
\( \Rightarrow {s_1} + {{\rm{v}}_1}({t_3} - {t_2}) = {s_2} + {{\rm{v}}_2}({t_3} - {t_2})\)
\(\Rightarrow15+3(t_3-5)=10+4(t_3-5)\)
\(\Rightarrow t_3=10\) s
Vậy kể từ lúc xuất phát tới khi người B đuổi kịp người A mất thời gian là 10 s.
c. Quãng đường người B đã đi trong khoảng thời gian đi với tốc độ không đổi (đến khi gặp nhau) là:
\({s_2}' = {{\rm{v}}_2}({t_3} - {t_2}) = 4.(10 - 5) = 20\) m
4. Trước khi đi vào đường cao tốc, người ta làm một đoạn đường nhập làn để ô tô có thể tăng tốc. Giả sử rằng một ô tô bắt đầu vào một đoạn đường nhập làn với tốc độ 36 km/h, tăng tốc với gia tốc 4,0 m/s2, đạt tốc độ 72 km/h khi hết đường nhập làn để bắt đầu vào đường cao tốc. Tính độ dài tối thiểu của đường nhập làn.
Hướng dẫn:
Vận tốc ban đầu: v0 = 36 km/h = 10 m/s
Vận tốc sau khi nhập làn: v = 72 km/h = 20 m/s
Độ dài tối thiểu của đường nhập làn là:
\(s = \frac{{{{\rm{v}}^2} - {\rm{v}}_0^2}}{{2{\rm{a}}}} = \frac{{{{20}^2} - {{10}^2}}}{{2.4}} = 37,5\) m
5. Hai xe ô tô A và B chuyển động thẳng cùng chiều. Xe A đang đi với tốc độ không đổi 72 km/h thì vượt xe B tại thời điểm t = 0. Để đuổi kịp xe A, xe B đang đi với tốc độ 45 km/h ngay lập tức tăng tốc đều trong 10 s để đạt tốc độ không đổi 90 km/h. Tính:
a) Quãng đường xe A đi được trong 10 s đầu tiên, kể từ lúc t = 0.
b) Gia tốc và quãng đường đi được của xe B trong 10 s đầu tiên.
c) Thời gian cần thiết để xe B đuổi kịp xe A.
d) Quãng đường mỗi ô tô đi được, kể từ lúc t = 0 đến khi hai xe gặp nhau.
Hướng dẫn:
Đổi đơn vị: 72 km/h = 20 m/s; 45 km/h = 12,5 m/s; 90 km/h = 25 m/s
a. Quãng đường xe A đi được trong 10 s đầu tiên, kể từ lúc t = 0 là:
\({s_A} = {v_A}.\Delta t = 20.10 = 200\) m
b. Vận tốc ban đầu của xe B là v1B = 12,5 m/s
Vận tốc sau khi xe B tăng tốc là v2B = 25 m/s
Gia tốc xe B trong 10 s đầu tiên: \(a = \frac{{{{\rm{v}}_{2B}} - {{\rm{v}}_{1B}}}}{{\Delta t}} = \frac{{25 - 12,5}}{{10}} = 1,25\) m/s2
Quãng đường đi được của xe B trong 10 s đầu tiên:
\(s = {{\rm{v}}_{1B}}.\Delta t + \frac{1}{2}a.\Delta {t^2} = 12,5.10 + \frac{1}{2}.1,{25.10^2} = 187,5\) m
c. Gọi khoảng thời gian cần thiết để xe B đuổi kịp xe A kể từ thời điểm t = 0 là
Quãng đường xe A đi được đến khi gặp nhau là:
\(s_A=v_A.\Delta t'=20.\Delta t'\)
Quãng đường xe B đi được đến khi gặp nhau là:
\({s_B} = {{\rm{v}}_{1B}}.\Delta t' + \frac{1}{2}a.\Delta t{'^2} = 12,5.\Delta t' + \frac{1}{2}.1,25.\Delta t'\)
Do 2 xe di chuyển cùng chiều, không đổi hướng nên tính từ thời điểm t = 0 đến khi gặp nhau thì quãng đường di chuyển của 2 xe bằng nhau:
\({s_A} = {s_B} \Rightarrow 20.\Delta t' = 12,5.\Delta t' + \frac{1}{2}.1,25.\Delta t{'^2} \Rightarrow \Delta t' = 12\) s
Vậy thời gian cần thiết là 12 giây (tính từ lúc xe A vượt xe B) để xe B đuổi kịp xe A.
d. Quãng đường mỗi xe đi được khi 2 xe gặp nhau là:
\(s_B=s_A=v_A.\Delta t'=20.12=240\) m
6. Hình 1 biểu diễn đồ thị vận tốc – thời gian của một quả bóng thả rơi chạm đất rồi nảy lên theo phương thẳng đứng. Quả bóng được thả tại A và chạm đất tại B. Quả bóng rời khỏi mặt đất tại D và đạt độ cao cực đại tại E. Có thể bỏ qua tác dụng của lực cản không khí.
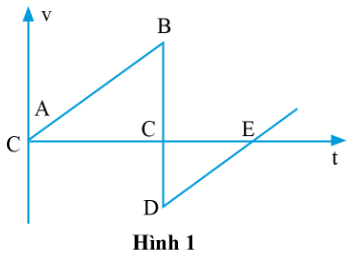
a) Tại sao độ dốc của đoạn thẳng AB lại giống độ dốc của đoạn thẳng DE?
b) Diện tích tam giác ABC biểu thị đại lượng nào?
c) Tại sao diện tích tam giác ABC lớn hơn diện tích tam giác CDE.
Hướng dẫn:
a) Chọn chiều dương là chiều từ trên xuống dưới, phương thẳng đứng.
Đoạn AB cho thấy độ lớn vận tốc tăng dần đều theo thời gian, do đó chuyển động là chuyển động nhanh dần đều, chiều từ trên xuống (cùng chiều dương)
Đoạn DE cho thấy độ lớn vận tốc giảm dần đều theo thời gian, do đó chuyển động là chuyển động chậm dần đều, ngược chiều dương đã chọn.
⇒ Cả 2 đoạn AB, DE đều là chuyển động thẳng biến đổi đều nên có gia tốc không đổi.
Mà độ dốc của đồ thị vận tốc - thời gian có giá trị bằng gia tốc của chuyển động. Do đó độ dốc của hai đoạn AB, DE giống nhau.
b) Diện tích tam giác ABC biểu thị đại lượng độ dịch chuyển khi quả bóng chuyển động từ điểm A (vị trí được thả) đến điểm B (vị trí chạm đất), đồng thời độ dịch chuyển này bằng với quãng đường từ A đến B vì trong giai đoạn này quả bóng chuyển động theo một hướng xác định.
c) Vì trong quá trình chuyển động rơi của quả bóng, một phần năng lượng ban đầu đã bị chuyển hóa thành nhiệt năng, năng lượng âm thanh khi chạm đất nên năng lượng của quả bóng bị giảm đi trong quá trình nảy lên. Do đó quả bóng không thể đạt đến độ cao ban đầu khi được thả, nên độ dịch chuyển khi chuyển động từ D (vị trí rời mặt đất) đến điểm E (độ cao cực đại) nhỏ hơn độ dịch chuyển khi quả bóng chuyển động từ điểm A đến điểm B.
7. Một quả bóng được thả rơi từ độ cao 1,20 m. Sau khi chạm đất, quả bóng bật lên ở độ cao 0,80 m. Thời gian tiếp xúc giữa bóng và mặt đất là 0,16 s. Lấy g = 9,8 m/s2. Bỏ qua sức cản của không khí. Tìm:
a) Tốc độ của quả bóng ngay trước khi chạm đất.
b) Tốc độ của quả bóng ngay khi bắt đầu bật lên.
c) Độ lớn và phương gia tốc của quả bóng trong khi tiếp xúc với mặt đất.
Hướng dẫn:
Chọn trục tọa độ Ox có phương thẳng đứng, chiều từ trên xuống.
a. Ta có: \({v^2} - v_0^2 = 2g{\rm{s}}\)
Do vật được thả rơi nên: \(v_0=0\)
Vậy vận tốc quả bóng ngay trước khi chạm đất là:
\(v = \sqrt {2g{\rm{s}}} = \sqrt {2.9,8.1,2} = 4,85\) m/s
Vì trong quá trình từ lúc được thả rơi đến ngay trước khi chạm đất, vật chuyển động thẳng, không đổi chiều, nên vận tốc của quả bóng cũng là tốc độ của nó. Do đó tốc độ của quả bóng ngay trước khi chạm đất là 4,85 m/s.
b. Thời gian tiếp xúc giữa bóng và mặt đất là 0,16 s. Khi chạm đất, đất là nguyên nhân làm cho quả bóng bị cản lại, gia tốc khi đó là a = -g, nên tốc độ của bóng ngay khi bắt đầu bật lên là:
\({v_1} = v - gt = 4,85 - 9,8.0,16 = 3,28\) m/s