Bài 9. Chuyển động thẳng biến đổi đều
Nội dung lý thuyết
Các phiên bản khácI. Gia tốc của chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi đều là chuyển động thẳng mà vận tốc có độ lớn tăng hoặc giảm đều theo thời gian.
Chuyển động thẳng nhanh dần đều là chuyển động thẳng có độ lớn vận tốc tăng đều theo thời gian.
Chuyển động thẳng chậm dần đều là chuyển động thẳng có độ lớn vận tốc giảm đều theo thời gian.
Vì chuyển động thẳng biến đổi đều có vận tốc thay đổi đều theo thời gian nên gia tốc không đổi theo thời gian:
\(a=\dfrac{\Delta\text{v}}{\Delta t}=\)
@2550011@
II. Vận tốc tức thời của chuyển động thẳng biến đổi đều
Gọi \(\text{v}_0\) là vận tốc tại thời điểm ban đầu \(t_0\), \(\text{v}_t\) là vận tốc tại thời điểm \(t\).
Vì \(a=\dfrac{\Delta\text{v}}{\Delta t}=\dfrac{\text{v}_t-\text{v}_0}{t-t_0}=\dfrac{\text{v}_t-\text{v}_0}{\Delta t}\) nên \(\text{v}_t=\text{v}_0+a.\Delta t\)
Nếu ở thời điểm ban đầu \(t_0=0\) thì: \(\text{v}_t=\text{v}_0+a.t\)
Nếu ở thời điểm ban đầu \(t_0=0\) vật mới bắt đầu chuyển động thì: \(\text{v}_0=0\) và \(\text{v}_t=a.t\)
III. Đồ thị vận tốc – thời gian của chuyển động thẳng biến đổi đều
Vận tốc tức thời v trong chuyển động thẳng biến đổi đều là hàm bậc nhất của thời gian t, nên đồ thị vận tốc – thời gian của chuyển động này có các dạng như sau:
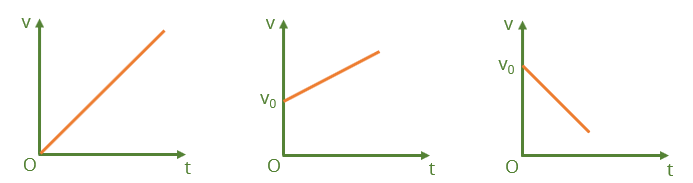
Các dạng đồ thị vận tốc - thời gian trong chuyển động thẳng biến đổi đều
@2550097@
IV. Độ dịch chuyển của chuyển động thẳng biến đổi đều
1. Tính độ dịch chuyển bằng đồ thị vận tốc – thời gian (v - t)
- Trong khoảng thời gian t, nếu vật chuyển động thẳng đều với vận tốc v, thì đồ thị (v – t) có dạng như hình dưới đây và độ dịch chuyển trong thời gian này có độ lớn là: \(d=\text{v}.t\).

Độ lớn này bằng diện tích của của hình chữ nhật, các cạnh có độ dài là v và t. Diện tích này gọi là diện tích giới hạn của đồ thị (v – t) đối với trục hoành.
- Trong thời gian t, nếu vật chuyển động thẳng biến đổi đều với vận tốc ban đầu v0 thì công thức tính vận tốc là \(\text{v}_t=\text{v}_0+a.t\), đồ thị (v – t) có dạng như hình dưới đây.

Có thể dựa vào đồ thị này để tính độ dịch chuyển.
Kẻ các đường song song với trục tung Ov, cách nhau một khoảng ∆t rất nhỏ để chia đồ thị thành các hình thang nhỏ có đường cao ∆t.
Chọn một hình thang nhỏ bất kì trong hình. Vì vật chuyển động thẳng biến đổi đều nên trong khoảng thời gian nhỏ từ tA đến tB, có thể coi chuyển động của vật là thẳng đều với vận tốc \(\text{v}_C=\dfrac{\text{v}_A+\text{v}_B}{2}\) (C nằm giữa A và B).
Độ dịch chuyển của vật trong thời gian ∆t có độ lớn bằng diện tích hình chữ nhật có cạnh là vC và ∆t. Hình vẽ cho thấy diện tích của hình này bằng điện thích của hình thang nhỏ gạch chéo có đường cao ∆t và các đáy có độ dài vA, vB.
Độ dịch chuyển trong thời gian t, bằng tổng các độ dịch chuyển trong các khoảng thời gian ∆t, nên có độ lớn bằng diện tích của hình thang vuông có đường cao là t và các đáy có độ lớn v0, v.
2. Tính độ dịch chuyển bằng công thức
Công thức tính độ lớn của độ dịch chuyển trong chuyển động thẳng biến đổi đều là:
\(d=\text{v}_0.t+\dfrac{1}{2}.a.t^2\)
Mặt khác: \(\text{v}_t=\text{v}_0+a.t\)
Suy ra: \(\text{v}_t^2-\text{v}_0^2=2.a.d\)
1. Chuyển động thẳng biến đổi đều là chuyển động thẳng có gia tốc không đổi theo thời gian.
2. Chuyển động thẳng nhanh dần đều có (a.v) > 0, chuyển động thẳng chậm dần đều có (a.v) < 0.
3. Hệ số góc của đồ thị vận tốc – thời gian của chuyển động thẳng biến đổi đều cho biết giá trị của gia tốc.
4. Các công thức của chuyển động thẳng biến đổi đều:
\(\text{v}_t=\text{v}_0+a.t\)
\(d=\text{v}_0.t+\dfrac{1}{2}.a.t^2\)
\(\text{v}_t^2-\text{v}_0^2=2.a.d\)