Hình trên mô tả sự thay đổi vị trí và vận tốc của ô tô, người sau những khoảng thời gian bằng nhau. Hai chuyển động này có gì giống nhau, khác nhau.
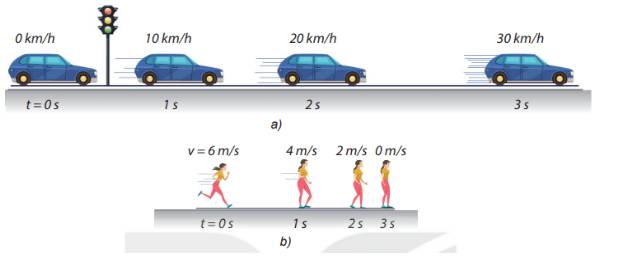
Hình trên mô tả sự thay đổi vị trí và vận tốc của ô tô, người sau những khoảng thời gian bằng nhau. Hai chuyển động này có gì giống nhau, khác nhau.

1. Tính gia tốc của các chuyển động trong hình vẽ ở đầu bài.
2. Các chuyển động trong hình vẽ ở đầu bài có phải là chuyển động thẳng biến đổi đều hay không?
1. Đối với hình (a):
Từ thời điểm 0s đến 1s: \(a_1=\dfrac{v_1-v_0}{t_1-t_0}=\dfrac{\dfrac{10}{3,6}-0}{1-0}=\dfrac{25}{9}\left(m/s^2\right)\)
Từ thời điểm 1s đến 2s: \(a_2=\dfrac{v_2-v_1}{t_2-t_1}=\dfrac{\dfrac{20}{3,6}-\dfrac{10}{3,6}}{2-1}=\dfrac{25}{9}\left(m/s^2\right)\)
Từ thời điểm 2s đến 3s: \(a_3=\dfrac{v_3-v_2}{t_3-t_2}=\dfrac{\dfrac{30}{3,6}-\dfrac{20}{3,6}}{3-2}=\dfrac{25}{9}\left(m/s^2\right)\)
Đối với hình (b):
Từ thời điểm 0s đến 1s: \(a_1=\dfrac{v_1-v_0}{t_1-t_0}=\dfrac{4-6}{1-0}=-2\left(m/s^2\right)\)
Từ thời điểm 1s đến 2s: \(a_2=\dfrac{v_2-v_1}{t_2-t_1}=\dfrac{2-4}{1-0}=-2\left(m/s^2\right)\)
Từ thời điểm 2s đến 3s: \(a_3=\dfrac{v_3-v_2}{t_3-t_2}=\dfrac{0-2}{3-2}=-2\left(m/s^2\right)\)
2. Đối với hình (a): Xe ô tô chuyển động thẳng, cứ 1s thì độ lớn vận tốc của xe ô tô tăng thêm \(2km/h\) nên chuyển động của xe ô tô là chuyển động thẳng biến đổi đều.
Đối với hình (b): Người chuyển động thẳng, cứ 1s thì độ lớn vận tốc của người giảm bớt \(2m/s\) nên chuyển động của người là chuyển động thẳng biến đổi đều.
Trả lời bởi Tô Mì1. Từ các đồ thị trong hình 9.1: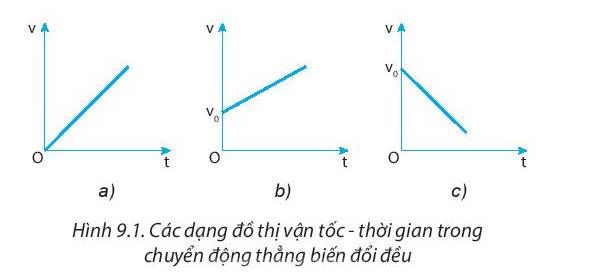
a) Hãy viết công thức về mối liên hệ giữa v với a và t của từng chuyển động ứng với từng đồ thị trong hình 9.1.
b) Chuyển động nào là chuyển động nhanh dần đều, chậm dần đều?
2. Hình 9.2 là đồ thị vận tốc – thời gian trong chuyển động của một bạn đang đi trong siêu thị. Hãy dựa vào đồ thị để mô tả bằng lời chuyển động của bạn đó (khi nào đi đều, đi nhanh lên, đi chậm lại, nghỉ).
1. (a)
Đồ thị hình a là đường thẳng đi qua gốc tọa độ nên công thức mối liên hệ giữa v, a và t có dạng hàm số \(y=ax\). Công thức cần tìm là: \(v=at\left(a>0\right)\).
Đồ thị hình b là đường thẳng xuất phát từ điểm \(v_0\) cách gốc tọa độ một khoảng đúng bằng \(v_0\) nên công thức mối liên hệ có dạng hàm số \(y=ax+b\left(a>0\right)\) (do đồ thị có dạng dấu sắc (đồng biến)) nên công thức cần tìm là: \(v=v_0+at\).
Đồ thị hình b là đường thẳng xuất phát từ điểm \(v_0\) cách gốc tọa độ một khoảng đúng bằng \(v_0\) nên công thức mối liên hệ có dạng hàm số \(y=ax+b\left(a< 0\right)\) (do đồ thị có dạng dấu huyền (nghịch biến)) nên công thức cần tìm là: \(v=v_0-at\).
(b) Chuyển động nhanh dần đều là các chuyển động ở hình a, b. Chuyển động chậm dần đều là chuyển động ở hình c.
2. Từ thời điểm 0s đến 4s, tức 4s đầu, bạn đi đều với tốc độ 1,5m/s.
Từ thời điểm 4s đến 6s, tức 2s tiếp theo, bạn bắt đầu đi chậm lại từ tốc độ 1,5m/s xuống 0m/s.
Sau đó, từ thời điểm 6s đến 7s, tức 1s tiếp theo, bạn này dừng lại.
Trong 1s tiếp theo, từ thời điểm 7s đến 8s, bạn này bắt đầu đảo chiều đi (đi ngược lại so với chiều đi ban đầu) và bắt đầu chuyển động nhanh dần từ tốc độ 0m/s đến 0,5m/s.
Trong 1s sau đó, từ thời điểm 8s đến 9s, bạn này đi đều với tốc độ 0,5m/s với chiều đi như giây trước.
Cuối cùng, từ thời điểm 9s đến 10s, tức 1s cuối, bạn này đi chậm lại từ tốc độ 0,5m/s và dừng hẳn (tốc độ 0m/s).
Trả lời bởi Tô Mì1. Hãy tính độ dịch chuyển của chuyển động có đồ thị (v-t) vẽ ở Hình 9.3b. Biết mỗi cạnh của ô vuông nhỏ trên trục tung ứng với 2 m/s, trên trục hoành ứng với 1 s.

2. Chứng tỏ rằng có thể xác định được giá trị của gia tốc dựa trên đồ thị (v - t).
1.
Độ dịch chuyển có độ lớn bằng diện tích của hình thang vuông có đường cao là t và các đáy có độ lớn v0, v.
Từ đồ thị ta có: \(\left\{ \begin{array}{l}{v_0} = 4\left( {m/s} \right);v = 16\left( {m/s} \right)\\t = 6\left( s \right)\end{array} \right.\)
Suy ra: Độ dịch chuyển là:
\(d = \frac{{\left( {4 + 16} \right).6}}{2} = 60\left( m \right)\)
Trả lời bởi Quoc Tran Anh Le1. Biết độ dịch chuyển trong chuyển động thẳng biến đổi đều có độ lớn bằng diện tích giới hạn đồ thị (v – t) trong thời gian t của chuyển động và các trục tọa độ. Hãy chứng minh rằng công thức tính độ lớn của độ dịch chuyển trong chuyển động thẳng biến đổi đều là:
d = vot + \(\dfrac{1}{2}\)at2 (9.4)
2. Từ công thức (9.2) và (9.4) chứng minh rằng:
v2−vo2 = 2.a.d (9.5)
1. Lấy ví dụ minh họa đồ thị hình 9.3 (SGK tr. 41).
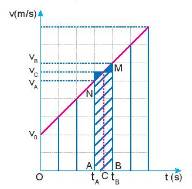
Ta sẽ tính độ dịch chuyển \(d\) của chất điểm có đồ thị vận tốc - thời gian như hình 9.3 trên.
Như đã biết theo đầu bài, độ dịch chuyển của chất điểm có độ lớn bằng với diện tích hình thang giới hạn bởi đồ thị (v - t) và trục tọa độ Ov, Ot.
Từ đồ thị, ta thấy được đáy nhỏ của hình thang có độ lớn là \(v_0\), đáy lớn của hình thang có độ lớn là \(v\) và chiều cao của hình thang có độ lớn là thời gian \(t\).
Công thức tính diện tích hình thang là: \(S=\dfrac{1}{2}\left(a+b\right)h\) với \(a,b,h\) lần lượt là độ dài đáy nhỏ, đáy lớn và chiều cao.
Áp dụng vào bài toán, ta được: \(d=S=\dfrac{1}{2}\left(v+v_0\right)t\)
\(=\dfrac{1}{2}vt+\dfrac{1}{2}v_0t\).
Mà: \(v=v_0+at\), thay vào ta được:
\(d=\dfrac{1}{2}\left(v_0+at\right)t+\dfrac{1}{2}v_0t\)
\(\Rightarrow d=\dfrac{1}{2}v_0t+\dfrac{1}{2}at^2+\dfrac{1}{2}v_0t\)
\(\Rightarrow d=v_0t+\dfrac{1}{2}at^2\) (điều phải chứng minh).
2. Ta có: \(\left\{{}\begin{matrix}v=v_0+at\\d=v_0t+\dfrac{1}{2}at^2\end{matrix}\right.\)
\(\Rightarrow v^2-v_0^2=\left(v+v_0\right)\left(v-v_0\right)\)
\(=\left(v_0+at+v_0\right)\left(v_0+at-v_0\right)\)
\(=at\left(2v_0+at\right)\)
\(=2a\left(v_0t+\dfrac{1}{2}at^2\right)=2ad\) (điều phải chứng minh).
Trả lời bởi Tô Mì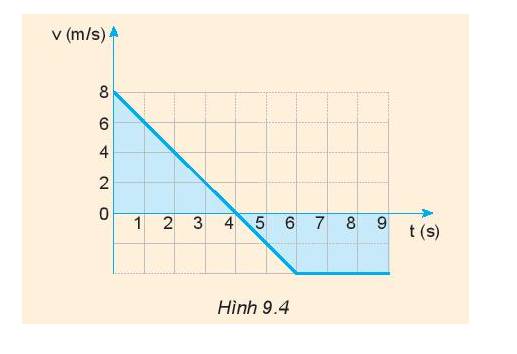
Hãy dùng đồ thị (v – t) vẽ ở hình 9.4 để:
a) Mô tả chuyển động
b) Tính độ dịch chuyển trong 4 giây đầu, 2 giây tiếp theo và 3 giây cuối
c) Tính gia tốc của chuyển động trong 4 giây đầu
d) Tính gia tốc của chuyển động từ giây thứ 4 đến giây thứ 6.
Kiểm tra kết quả của câu b và câu c bằng cách dùng công thức.
a) Mô tả chuyển động:
- Trong 4 giây đầu tiên: chuyển động chậm dần đều từ 8 m/s đến 0 m/s
- Từ giây thứ 4 đến giây thứ 6: bắt đầu tăng tốc với vận tốc -2 m/s
- Từ giây thứ 6 đến giây thứ 9: chuyển động thẳng đều với vận tốc – 2 m/s
b) Độ dịch chuyển:
- Trong 4 giây đầu:
Độ dịch chuyển bằng diện tích tam giác vuông có cạnh đáy là t và chiều cao là v.
\({d_1} = \frac{1}{2}.{t_1}.{v_1} = \frac{1}{2}.4.8 = 16\left( m \right)\)
- Trong 2 giây tiếp theo:
Độ dịch chuyển bằng diện tích tam giác vuông có cạnh đáy là t và chiều cao là v.
\({d_2} = \frac{1}{2}.{t_2}.{v_2} = \frac{1}{2}.2.( - 4) = - 4\left( m \right)\)
- Trong 3 giây cuối:
Độ dịch cuyển bằng diện tích hình chữ nhật có chiều dài là t và chiều rộng là v.
\({d_3} = {v_3}.{t_3} = - 4.3 = - 12\left( m \right)\)
c)
Gia tốc của chuyển động trong 4 giây đầu:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{0 - 8}}{{4 - 0}} = - 2\left( {m/{s^2}} \right)\)
d)
Gia tốc của chuyển động từ giây thứ 4 đến giây thứ 6:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{ - 4 - 0}}{{6 - 4}} = - 2\left( {m/{s^2}} \right)\)
* Kiểm tra kết quả bằng công thức:
Độ dịch chuyển:
- Trong 4 giây đầu:
\({d_1} = {v_0}.{t_1} + \frac{1}{2}.a.t_1^2 = 8.4 + \frac{1}{2}.( - 2){.4^2} = 16(m)\)
- Trong 2 giây tiếp theo:
\({d_2} = {v_0}{t_2} + \frac{1}{2}a{t_2}^2 = 0.2 + \frac{1}{2}.( - 2){.2^2} = - 4\left( m \right)\)
- Trong 3 giây cuối:
\({d_3} = {v_3}t = - 4.3 = - 12\left( m \right)\)
=> Trùng với kết quả khi dùng đồ thị.
Trả lời bởi Quoc Tran Anh Le1. Đồ thị vận tốc – thời gian ở Hình 9.5 mô tả chuyển động của một chú chó con đang chạy trong một ngõ thẳng và hẹp.
a) Hãy mô tả chuyển động của chú chó.
b) Tính quãng đường đi được và độ dịch chuyển của chú chó sau: 2s; 4s; 7s và 10s bằng đồ thị và bằng công thức.
2. Một vận động viên đua xe đạp đường dài vượt qua vạch đích với tốc độ 10 m/s. Sau đó vận động viên này đi chậm dần đều thêm 20 m mới dừng lại. Coi chuyển động của vận động viên là thẳng.
a) Tính gia tốc của vận động viên trong đoạn đường sau khi qua vạch đích.
b) Tính thời gian vận động viên đó cần để dừng lại kể từ khi cán đích.
c) Tính vận tốc trung bình của người đó trên quãng đường dừng xe.
1.
a) Mô tả chuyển động:
- Trong 2 giây đầu tiên: chuyển động thẳng đều với vận tốc 1 m/s.
- Từ giây thứ 2 đến giây thứ 4: chuyển động nhanh dần đều
- Từ giây 4 đến giây 7: chuyển động chậm dần
- Từ giây 4 đến giây 8: dừng lại
- Từ giây 8 đến giây 9: chuyển động nhanh dần theo chiều âm
- Từ giây 9 đến giây 10 chuyển động thẳng đều với vận tốc -1 m/s.
b) Quãng đường đi được và độ dịch chuyển:
- Sau 2 giây:
\({s_1} = {d_1} = {v_1}{t_1} = 1.2 = 2\left( {m/s} \right)\)
- Sau 4 giây:
\({s_2} = {d_2} = {s_1} + \frac{1}{2}(1 + 3).2 = 2 + 4 = 6\left( m \right)\)
- Sau 7 giây:
+ Quãng đường:
\({s_3} = {s_2} + \frac{1}{2}.3.\left( {7 - 4} \right) = 6 + 4,5 = 10,5\left( m \right)\)
+ Độ dịch chuyển:
\({d_3} = {d_2} + \frac{1}{2}.(3).\left( {7 - 4} \right) = 6 + 4,5 = 10,5\left( m \right)\)
- Sau 10 giây:
+ Quãng đường:
\({s_4} = {s_3} + s' = 10,5 + 0,5 + 1 = 12\left( m \right)\)
+ Độ dịch chuyển:
\({d_4} = {d_3} + d' = 10,5 - 0,5 - 1 = 9\left( m \right)\)
* Kiểm tra bằng công thức:
- Sau 2 giây:
\({s_1} = {d_1} = {v_1}{t_1} = 1.2 = 2\left( {m/s} \right)\)
- Sau 4 giây:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{3 - 1}}{{4 - 2}} = \frac{2}{2} = 1\left( {m/{s^2}} \right)\)
\({s_2} = {d_2} = {d_1} + {v_1}{t_1} + \frac{1}{2}at_1^2 = 2 + 1.2 + \frac{1}{2}{.1.2^2} = 6\left( m \right)\)
- Sau 7 giây:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{0 - 3}}{{7 - 4}} = \frac{2}{2} = - 1\left( {m/{s^2}} \right)\)
+ Quãng đường và độ dịch chuyển từ giây 4 đến giây 7 là:
\(d' = s' = {v_0}t + \frac{1}{2}a{t^2} = 3.3 + \frac{1}{2}( - 1).{(7 - 4)^2} = 4,5\left( m \right)\)
=> Quãng đường và độ dịch chuyển đi được sau 7 giây là:
\({d_3} = {s_3} = {d_2} + d' = 6 + 4,5 = 10,5\left( m \right)\)
- Sau 10 giây:
+ Từ giây 7 – 8: đứng yên
+ Từ giây 8 – 9:
\(a = \frac{{ - 1 - 0}}{{9 - 8}} = - 1\left( {m/{s^2}} \right)\)
\(d = {v_0}t + \frac{1}{2}a{t^2} = 0.1 + \frac{1}{2}\left( { - 1} \right){.1^2} = - 0,5\left( m \right)\)
s = 0,5 m
+ Từ giây 9 – 10:
\(d = vt = - 1.1 = - 1\left( m \right)\)
s = 1 m
Suy ra: độ dịch chuyển và quãng đường đi được sau 10 giây lần lượt là:
\({d_4} = {d_3} - 0,5 - 1 = 10,5 - 0,5 - 1 = 9\left( m \right)\)
\({s_4} = {s_3} - 0,5 - 1 = 10,5 + 0,5 + 1 = 12\left( m \right)\)
=> Kiểm tra thấy các kết quả trùng nhau.
Trả lời bởi Quoc Tran Anh LeTừ đồ thị vận tốc – thời gian của chuyển động thẳng biến đổi đều mô tả được chuyển động này.
Ví dụ có đồ thị vận tốc – thời gian của một chuyển động.

Mô tả chuyển động:
- Từ giây thứ 0 đến giây thứ 2: chuyển động thẳng đều với vận tốc 1 m/s.
- Từ giây thứ 2 đến giây thứ 4: chuyển động thẳng nhanh dần đều từ 1 m/s đến 3 m/s.
- Từ giây thứ 4 đến giây thứ 7: chuyển động chậm dần đều từ 3 m/s về 0 m/s.
- Từ giây thứ 7 đến giây thứ 8: đứng yên.
- Từ giây thứ 8 đến giây thứ 9: chuyển động thẳng nhanh dần đều theo chiều ngược lại (theo chiều âm).
- Từ giây thứ 9 đến giây thứ 10: chuyển động thẳng đều theo chiều âm.
Trả lời bởi Quoc Tran Anh Le
- Giống: đều là chuyển động thẳng và có gia tốc không thay đổi.
- Khác nhau:
+ Chuyển động của ô tô có vận tốc tăng dần đều sau những khoảng thời gian bằng nhau nên đây là chuyển động nhanh dần đều.
+ Chuyển động của người có vận tốc giảm dần đều nên đây là chuyển động chậm dần đều.
Trả lời bởi Quoc Tran Anh Le