Bài 4: Hai mặt phẳng vuông góc
Nội dung lý thuyết
Các phiên bản khácI. GÓC GIỮA HAI MẶT PHẲNG
1. Định nghĩa
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
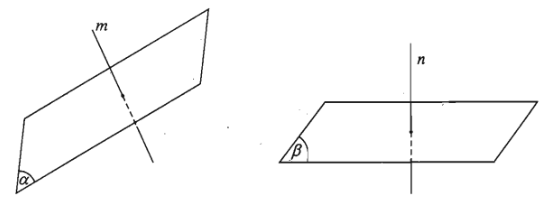
Nếu hai mặt phẳng song song hoặc trùng nhau thì ta nói góc giữa hai mặt phẳng đó bằng \(0^0\).
2. Cách xác định góc giữa hai mặt phẳng cắt nhau
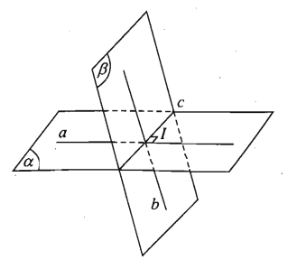
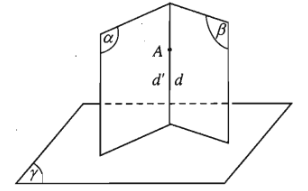
Giả sử hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) cắt nhau theo giao tuyến \(c\). Từ một điểm \(I\) bất kì trên \(c\) ta dựng trong \(\left(\alpha\right)\) một đường thẳng \(a\) vuông góc với \(c\) và dựng trong \(\left(\beta\right)\) một đường thẳng \(b\) vuông góc với \(c\).
Góc giữa hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) là góc giữa hai đường thẳng \(a\) và \(b\).
3. Diện tích hình chiếu của một đa giác
Cho đa giác \(H\) nằm trong mặt phẳng \(\left(\alpha\right)\) có diện tích \(S\) và \(H'\) là hình chiếu vuông góc của \(H\) trên mặt phẳng \(\left(\beta\right)\). Khi đó diện tích \(S'\) của \(H'\) được tính theo công thức:
\(S'=S\cos\varphi\)
với \(\varphi\) là góc giữa \(\left(\alpha\right)\) và \(\left(\beta\right)\).
Ví dụ 1: Cho hình chóp \(S.ABC\) có đáy là tam giác đều \(ABC\) cạnh \(a\), cạnh bên \(SA\perp mp\left(ABC\right)\) và \(SA=\dfrac{a}{2}\)
a) Tính góc giữa hai mặt phẳng \(\left(ABC\right)\) và \(\left(SBC\right)\) ;
b) Tính diện tích tam giác \(SBC\).
Giải:
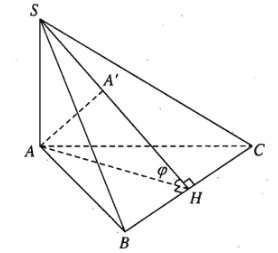
a) Gọi \(H\) là trung điểm cạnh \(BC\). Ta có \(BC\perp AH\) (1)
Vì \(SA\perp\left(ABC\right)\) nên \(SA\perp BC\) (2)
Từ (1) và (2) suy ra \(BC\perp\left(SAH\right)\Rightarrow BC\perp SH\)
Vậy góc giữa hai mặt phẳng \(\left(ABC\right)\) và \(\left(SBC\right)\) là \(\widehat{SHA}\).
Đặt \(\varphi=\widehat{SHA}\) ta có: \(\tan\varphi=\dfrac{SA}{AH}=\dfrac{\dfrac{a}{2}}{\dfrac{a\sqrt{3}}{2}}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\).
Suy ra \(\varphi=30^0\).
b) Vì \(SA\perp\left(ABC\right)\) nên tam giác \(ABC\) là hình chiếu vuông góc của tam giác \(SBC\). Gọi \(S_1,S_2\) lần lượt là diện tích tam giác \(SBC\) và \(ABC\). Ta có: \(S_2=S_1.\cos\varphi\Rightarrow S_1=\dfrac{S_2}{\cos\varphi}\)
Suy ra \(S_1=\dfrac{2}{\sqrt{3}}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^2}{2}\).
@62276@
II. HAI MẶT PHẲNG VUÔNG GÓC
1. Định nghĩa
Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa hai mặt phẳng đó là góc vuông.
Nếu hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) vuông góc với nhau ta kí hiệu là \(\left(\alpha\right)\perp\left(\beta\right)\).
2. Các định lí
- Định lí 1:
Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
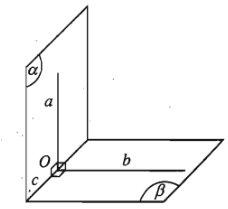
Hệ quả 1:
Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến thì vuông góc với đường thẳng kia.
Hệ quả 2:
Cho hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) vuông góc với nhau. Nếu từ một điểm thuộc mặt phẳng \(\left(\alpha\right)\) ta dựng một đường thẳng vuông góc với mặt phẳng \(\left(\beta\right)\) thì đường thẳng này nằm triong mp \(\left(\alpha\right)\).
- Định lí 2:
Nếu hai mặt phẳng vuông góc nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.
@62288@
III. HÌNH LĂNG TRỤ ĐỨNG, HÌNH HỘP CHỮ NHẬT, HÌNH LẬP PHƯƠNG
1. Định nghĩa
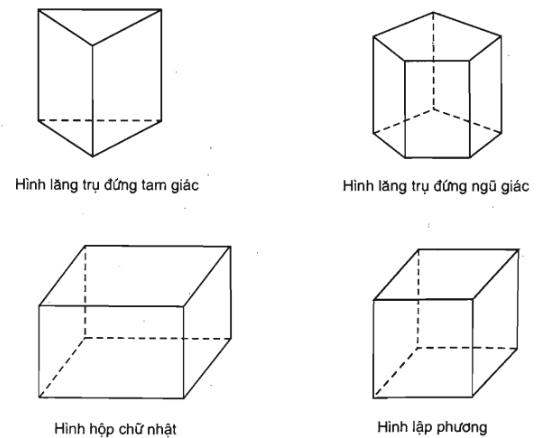
Hình lăng trụ đứng là hình lăng trụ có các mặt bên vuông góc với các mặt đáy.
- Hình lăng trụ đứng có đáy là các tam giác, tứ giác, ngũ giác,... được gọi là hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác, hình lăng trụ đứng ngũ giác,...
- Hình lăng trụ đứng có đáy là một đa giác đều được gọi là hình lăng trụ đều. Ta có các lại hình lăng trụ đều như hình lăng trụ tam giác đều, hình lăng trụ tứ giác đều, hình lăng trụ ngũ giác đều,...
- Hình lăng trụ đứng có đáy là hình bình hành được gọi là hình hộp đứng.
- Hình lăng trụ đứng có đáy là hình chữ nhật được gọi là hình hộp chữ nhật.
- Hình lăng trụ đứng có đáy là hình vuông và các mặt bên là các hình vuông được gọi là hình lập phương.
2. Nhận xét
Các mặt bên của hình lăng trụ đứng luôn vuông góc với các mặt phẳng đáy và là những hình chữ nhật.
Ví dụ 2: Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Tính diện tích thiết diện của hình lập phương được cắt bởi mặt phẳng trung trực \(\left(\alpha\right)\) của đoạn \(AC'\).
Giải:
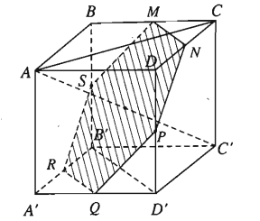
Gọi \(M\) là trung điểm \(BC\). Ta có \(MA=MC'=\dfrac{a\sqrt{5}}{2}\) nên \(M\) thuộc mặt phẳng trung trực \(\left(\alpha\right)\) của đoạn \(AC'\).
Gọi \(N,P,Q,R,S\) lần lượt là trung điểm các đoạn \(CD,DD',D'A',A'B',B'B\).
Tương tự như trên ta cũng chứng minh được các điểm \(N,P,Q,R,S\) đều thuộc mặt phẳng trung trực \(\left(\alpha\right)\) của đoạn \(AC'\).
Vậy thiết diện cần tìm là lục giác đều \(MNPQRS\) có cạnh bằng \(\dfrac{a\sqrt{5}}{2}\).
Diện tích \(S\) của tứ diện cần tìm là: \(S=6.\left(\dfrac{a\sqrt{2}}{2}\right)^2.\dfrac{\sqrt{3}}{4}=\dfrac{3\sqrt{3}}{4}a^2\).
IV. HÌNH CHÓP ĐỀU VÀ HÌNH CHÓP CỤT ĐỀU
1. Hình chóp đều
Một hình chóp được gọi là hình chóp đều nếu nó có đáy là một đa giác đều và có chân đường cao trùng với tâm của đa giác đáy.
Nhận xét:
- Hình chóp đều có các mặt bên là các tam giác cân bằng nhau, các mặt bên tạo với mặt đáy các góc bằng nhau.
- Các cạnh bên của hình chóp đều tạo với mặt đáy các góc bằng nhau.
2. Hình chóp cụt đều
Phần của hình chóp đều nằm giữa đáy và thiết diện song song với đáy cắt các cạnh bên của hình chóp đều được gọi là hình chóp cụt đều.
Nhận xét: Các mặt bên của hình chóp cụt đều là các hình thang cân và các cạnh bên của hình chóp cụt đều có độ dài bằng nhau.
@62283@