Bài 3: Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác

1. Bất đẳng thức tam giác

Định lí: 

Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.

Cụ thể: Cho tam giác \(ABC\), ta có các bất đẳng thức sau:

             \(AB+AC>BC\);

             \(AB+BC>AC\);

             \(AC+BC>AB\).

Chứng minh:

Ta chứng minh được bất đẳng thức đầu tiên, các bất đẳng thức còn lại chứng minh tương tự.

Trên tia đối của tia \(AB\), lấy điểm \(D\) sao cho \(AD=AC\). 

Khi đó \(BD=AB+AD=AB+AC\)

Do tia \(CA\) nằm giữa hai tia \(CB\) và \(CD\) nên \(\widehat{BCD}>\widehat{ACD}\)     (1)

Mặt khác, theo cách dựng ta có \(\Delta ACD\) cân tại \(A\) nên \(\widehat{ACD}=\widehat{ADC}=\widehat{BDC}\)       (2)

Từ (1) và (2) \(\Rightarrow\widehat{BCD}>\widehat{BDC}\)

Xét trong tam giác \(BCD\), ta có \(\widehat{BCD}>\widehat{BDC}\) 

\(\Rightarrow BD>BC\) (quan hệ giữa cạnh và góc trong tam giác)

Hay \(AB+AC>BC\) 

Ta chứng minh tương tự với các bất đẳng thức còn lại.

Ví dụ: Xét trong tam giác \(DEF\) bất kì, ta có các bất đẳng thức: 

        \(DE+DF>EF;DE+EF>DF;DF+EF>DE\)

Ví dụ 1: Xét các bộ ba sau, các bộ ba nào có thể là độ dài 3 cạnh của một tam giác?

     a) \(3cm,5cm,7cm\).

     b) \(4cm,5cm,6cm\).

     c) \(12,5cm;3,7cm;4,8cm\).

     d) \(4,5cm;1cm,3cm\)

Giải:

a) Xét bộ ba \(3cm,5cm,7cm\) ta có: \(\left\{{}\begin{matrix}3+5=8>7\\5+7=12>3\\3+7=10>5\end{matrix}\right.\) (thỏa mãn bất đẳng thức tam giác)

   Nên bộ ba \(3cm,5cm,7cm\) có thể lập thành một tam giác.

b) Xét bộ ba \(4cm,5cm,6cm\) ta có: \(\left\{{}\begin{matrix}4+5=9>6\\5+6=11>4\\4+6=10>5\end{matrix}\right.\) (thỏa mãn bất đẳng thức tam giác)

   Nên bộ ba \(4cm,5cm,6cm\) có thể lập thành một tam giác.

c) Xét bộ ba \(12,5cm;3,7cm;4,8cm\) ta có: \(\left\{{}\begin{matrix}12,5+3,7=16,2>4,8\\12,5+4,8=17,3>3,7\\3,7+4,8=8,5< 12,5\end{matrix}\right.\) (không thỏa mãn         bất đẳng thức tam giác) 

    Nên bộ ba \(12,5cm;3,7cm;4,8cm\) không thể lập thành một tam giác.

d) Xét bộ ba \(4,5cm;1cm,3cm\) ta có: \(\left\{{}\begin{matrix}4,5+1=5,5>3\\4,5+3=7,5>1\\1+3=4< 4,5\end{matrix}\right.\) (không thỏa mãn bất đẳng thức     tam giác) 

    Nên bộ ba \(4,5cm;1cm,3cm\) không thể lập thành một tam giác.

Ví dụ 2: Cho tam giác \(ABC\) (\(AB=AC\)) có đường cao \(AH\). Gọi \(D\) là một điểm nằm trên cạnh \(BC\). So sánh \(AH\), \(AD\), \(AB\)?

Giải:

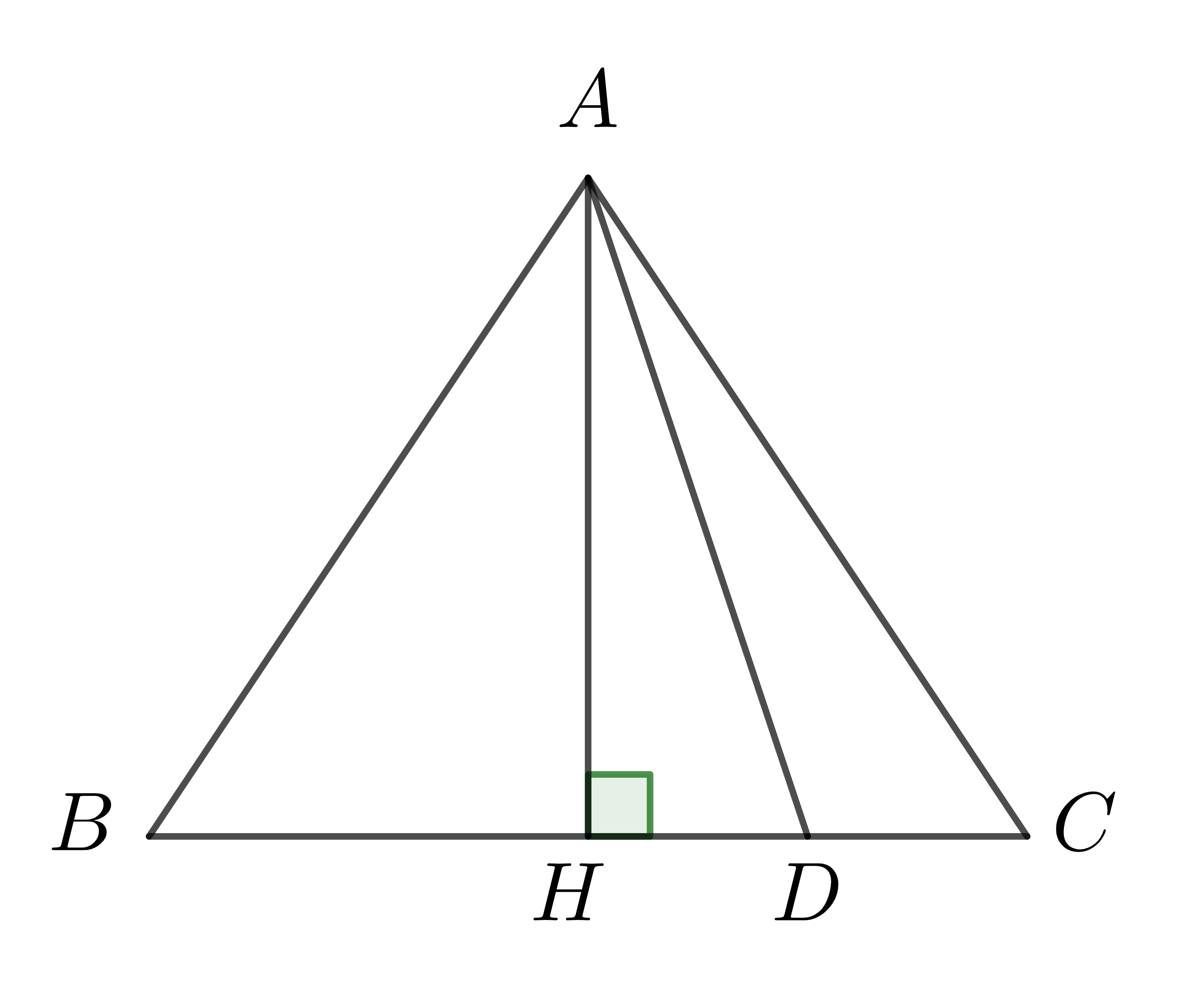
Ta có: \(AH< AD\)   (quan hệ giữa đường vuông góc và đường xiên)   (1)  

Lại có: \(\widehat{ADB}\) là góc ngoài đỉnh \(D\) của tam giác \(ADC\)

\(\Rightarrow\widehat{ADB}=\widehat{ACD}+\widehat{DAC}=\widehat{ACB}+\widehat{DAC}\)  

\(\Rightarrow\widehat{ADB}>\widehat{ACB}\)

Mà tam giác \(ABC\) cân (do \(AB=AC\)) \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)

Từ đó ta suy ra \(\widehat{ADB}>\widehat{ABC}\) hay \(\widehat{ADB}>\widehat{ABD}\)

Xét trong tam giác \(ABD\) có \(\widehat{ADB}>\widehat{ABD}\) 

\(\Rightarrow AB>AD\) (quan hệ giữa cạnh và góc trong tam giác)      (2)

Từ (1) và (2) suy ra \(AH< AD< AB\)

Ví dụ 3: Cho tứ giác \(ABCD\) có \(O\) là giao điểm 2 đường chéo. Viết biểu thức liên hệ giữa tổng độ dài các cạnh của tứ giác với tổng độ dài hai đường chéo?

Giải:

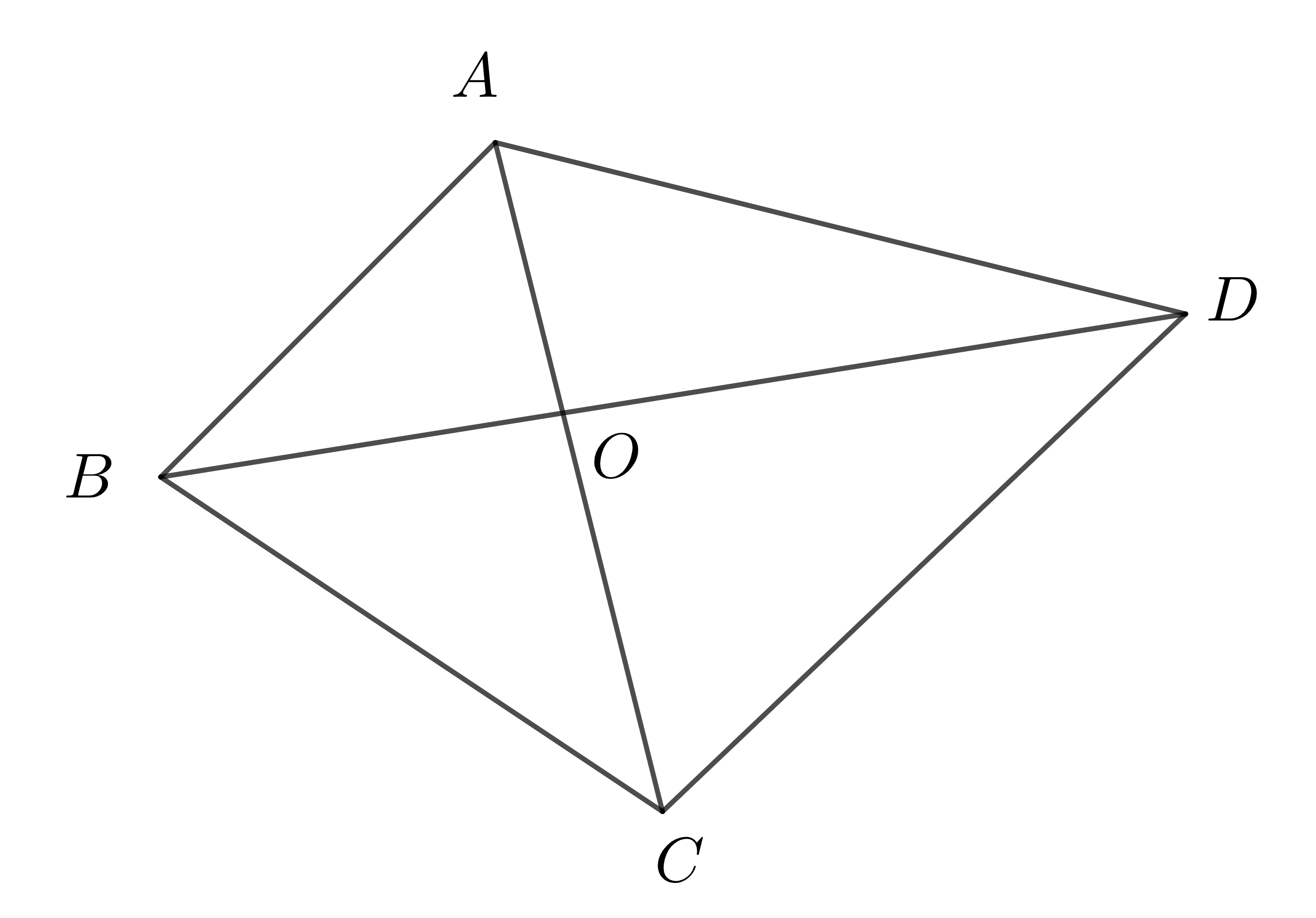
Xét trong tam giác \(OAB\) ta có: \(OA+OB>AB\)

Xét trong tam giác \(OBC\) ta có: \(OB+OC>BC\)

Xét trong tam giác \(OCD\) ta có: \(OC+OD>CD\)

Xét trong tam giác \(ODA\) ta có: \(OD+OA>DA\)

Cộng theo vế của các bất đẳng thức trên ta được: 

\(2\left(OA+OB+OC+OD\right)>AB+BC+CD+DA\)

\(\Rightarrow2\left(AC+BD\right)>AB+BC+CD+DA\)

\(\Rightarrow AC+BD>\dfrac{AB+BC+CD+DA}{2}\)

Hay \(\dfrac{AB+BC+CD+DA}{2}< AC+BD\)

2. Hệ quả của bất đẳng thức tam giác

Hệ quả:

Trong một tam giác, hiệu độ dài hai cạnh bất kì bao giờ cũng nhỏ hơn độ dài cạnh còn lại.

Cụ thể: Cho tam giác \(ABC\), ta có các bất đẳng thức hệ quả:

      \(AB-AC< BC;AC-AB< BC\);

      \(AB-BC< AC;BC-AB< AC\);

      \(AC-BC< AB;BC-AC< AB\).

Nhận xét: Nếu xét đồng thời cả tổng và hiệu độ dài hai cạnh của tam giác thì quan hệ giữa các cạnh của nó còn được phát biểu như sau:

Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn lại.

Chẳng hạn, với tam giác \(ABC\) ta có: 

        \(AB-AC< BC< AB+AC\)

        \(AC-BC< AB< AC+BC\)

        \(BC-AB< AC< BC+AB\)

Lưu ý: Khi xét độ dài ba đoạn thẳng có thỏa mãn bất đẳng thức tam giác hay không, ta chỉ cần so sánh độ dài lớn nhất với tổng hai độ dài còn lại, hoặc so sánh độ dài nhỏ nhất với hiệu hai độ dài còn lại.

Ví dụ: Xét bộ ba \(12cm,13cm,9cm\), ta thấy:

     +) \(13cm< 12cm+9cm\) nên bộ ba trên thỏa mãn bất đẳng thức tam giác;

     +) Hoặc \(9cm>13cm-12cm\) nên bộ ba trên thỏa mãn bất đẳng thức tam giác.

Ví dụ 1: Cho tam giác \(ABC\) có \(AB=7cm,AC=1cm\). Biết độ dài cạnh \(BC\) là một số nguyên. Tính chu vi tam giác \(ABC\)?

Giải:

Áp dụng bất đẳng thức trong tam giác và hệ quả của nó ta có:     

           \(AB-AC< BC< AB+AC\)

\(\Rightarrow7-1< BC< 7+1\)

\(\Rightarrow6< BC< 8\)

Mà độ dài \(BC\) là số nguyên nên \(BC=7\left(cm\right)\)

Do đó chu vi tam giác \(ABC\) là: \(AB+BC+CA=7+7+1=15\left(cm\right)\)