Đây là phiên bản do Cam Ngọc Tử Minh
đóng góp và sửa đổi vào 17 tháng 8 2023 lúc 20:25. Xem phiên bản hiện hành
Bài 2. Cộng, trừ, nhân, chia số hữu tỉ
Nội dung lý thuyết
Các phiên bản khác
1
3 gp
Bài 2: Cộng, trừ, nhân, chia số hữu tỉ
1. Cộng, trừ hai số hữu tỉ
- Cách cộng, trừ hai số hữu tỉ:
Mọi số hữu tỉ đều viết được dưới dạng phân số với mẫu dương nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.
Ví dụ:
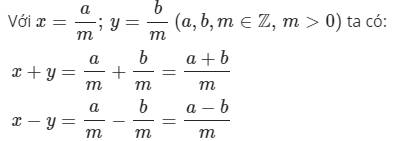
- Phép cộng số hữu tỉ cũng có các tính chất của phép cộng phân số:
+ Tính chất giao hoán: \(a+b=b+a\)
+ Tính chất kết hợp: \((a+b)+c = a + (b+c) = b + (c + a)\)
+ Tính chất cộng với số 0: \(a + 0 = a\)
- Mỗi số hữu tỉ chỉ có một số đối duy nhất, tổng của hai số hữu tỉ đối nhau bằng 0
Ví dụ: \((-a) + a = 0\)
\((-9) + 9 =0\)
2. Nhân, chia hai số hữu tỉ
- Cách nhân, chia hai số hữu tỉ:
Mọi số hữu tỉ đều viết được dưới dạng phân số với mẫu dương nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.
Ví dụ:
+ Phép nhân:
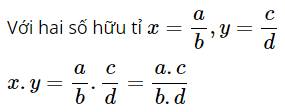
+ Phép chia
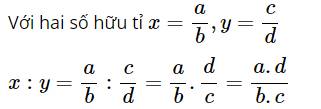
- Phép nhân số hữu tỉ cũng có các tính chất của phép nhân phân số:
+ Tính chất giao hoán: \(a.b=b.a\)
+ Tính chất kết hợp: \((a.b).c = a . (b.c) = b . (c . a)\)
+ Tính chất nhân với số 1: \(a . 1= a\)
+ Tính chất nhân với số 0: \(a.0=0\)
+ Tính chất phân phối giữa phép nhân và phép cộng: \(a.(b+c)=a.b + a.c\)
+ Tính chất phân phối giữa phép nhân và phép trừ: \(a.(b-c)=a.b - a.c\)
- Mỗi số hữu tỉ khi viết dưới dạng phân số chỉ có một phân số nghịch đảo duy nhất, tích của hai số hữu tỉ nghịch đảo bằng 1
Ví dụ: \(\dfrac{a}{b}.\dfrac{b}{a}=\dfrac{a.b}{b.a}=1\)
\(\dfrac{2}{3}.\dfrac{3}{2}=\dfrac{2.3}{3.2}=\dfrac{6}{6}=1\)
Danh sách các phiên bản khác của bài học này. Xem hướng dẫn
| Cam Ngọc Tử Minh đã đóng góp một phiên bản khác cho bài học này (17 tháng 8 2023 lúc 20:25) | 1 lượt thích |