Bài 1: Động lượng và định luật bảo toàn động lượng

I. Động lượng

Để xem xét ảnh hưởng của sự va chạm giữa các vật, người ta dùng thí nghiệm thả các viên bi có cùng kích thước nhưng có khối lượng khác nhau xuống một khối đất nặn. Căn cứ vào độ lún sâu của viên bi vào khối đất nặn, có thể đánh giá được tác động của viên bi đang chuyển động đối với vật cản là đất nặn.

Kết quả thí nghiệm cho thấy, với cùng một viên bi, tốc độ khi va chạm càng lớn, nó càng lún sâu vào đất nặn. Với các viên bi cùng kích thước, viên bi nào khối lượng càng lớn, càng lún sâu vào đất nặn.

Qua nhiều ví dụ, người ta thấy rằng có thể sử dụng đại lượng bằng tích của vận tốc và khối lượng để đặc trưng cho lượng chuyển động của vật trong tương tác, đại lượng này được gọi là động lượng. 

Động lượng = khối lượng x vận tốc

\(\overrightarrow{p}=m\times\overrightarrow{v}\)

Đơn vị của động lượng là kg.m/s

Hướng của động lượng theo hướng của vận tốc.

Động lượng là một đơn vị vecto, cùng hướng với vận tốc.

II. Định luật bảo toàn động lượng

1. Động lượng và định luật II Newton

Gia tốc chính là tốc độ thay đổi vận tốc. Từ định luật II Newton (lực bằng tích khối lượng với gia tốc của vật) và biểu thức \(\overrightarrow{p}=m\times\overrightarrow{v}\), rút ra lực tác dụng bằng tốc độ thay đổi động lượng. Do đó, định luật II Newton được phát biểu qua động lượng như sau :

Hợp lực tác dụng lên một vật bằng tốc độ thay đổi động lượng của nó.

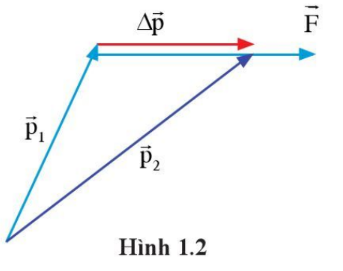
Hợp lực \(\overrightarrow{F}\) được xác định :

\(\overrightarrow{F}=\dfrac{\Delta\overrightarrow{p}}{\Delta t}\)

Với \(\Delta\overrightarrow{p}\) là độ thay đổi động lượng trong thời gian \(\Delta t\).

Hướng của hợp lực theo hướng của độ thay đổi động lượng (hình 1.2).

2. Định luật bảo toàn động lượng

Nếu không có ngoại lực nào tác dụng lên hệ thì tổng động lượng của hệ không đổi, tức là được bảo toàn.

\(\overrightarrow{p_1}+\overrightarrow{p_2}=\) không đổi

Hệ vật chỉ có những lực của các vật trong hệ tác dụng lẫn nhau, không có tác dụng của những lực từ bên ngoài hệ hoặc nếu có thì các lực này triệt tiêu lẫn nhau được gọi là hệ kín.

3. Thí nghiệm kiểm chứng định luật bảo toàn động lượng

Chúng ta có thể kiểm chứng định luật bảo toàn động lượng bằng thí nghiệm sau đây :

Đặt hai xe kĩ thuật số (gọi tắt là xe) có khối lượng bằng nhau lên giá đỡ nằm ngang. Cho xe 1 chuyển động va chạm vào xe 2 đang nằm yên. Sau va chạm hai xe dính vào nhau. Đọc và ghi tốc độ của từng xe trước và sau va chạm. Từ kết quả thu được, tính động lượng của hai xe trước và sau va chạm.

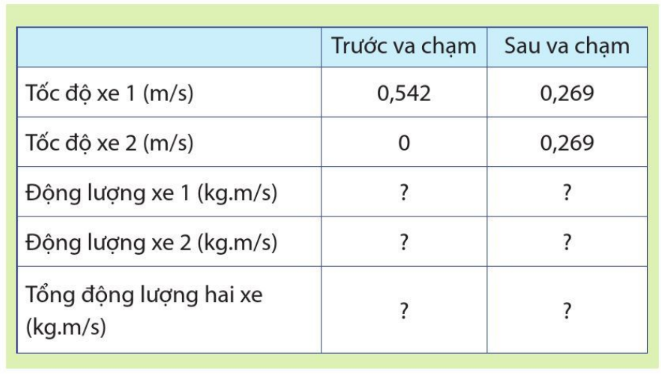
Từ kết quả ở bảng, đánh giá động lượng của hai xe trước và sau va chạm như sau :

Khối lượng của mỗi xe là 0,245kg.

Trước va chạm : Tốc độ của xe 1 là 0,542 m/s, động lượng của nó là 0,133 kg.m/s. Xe 2 đứng yên, động lượng bằng 0. Sau va chạm, hai xe có cùng tốc độ 0,269 m/s.

Tổng động lượng của hai xe trước va chạm là :

0,133 kg.m/s + 0 kg.m/s = 0,133 kg.m/s

Tổng động lượng của hai xe sau va chạm là :

0,066 kg.m/s + 0,066 kg.m/s = 0,132 kg.m/s

Kết quả cho thấy :

Tổng động lượng của hai xe sau va chạm bằng 99,2% tổng động lượng của hai xe trước va chạm. Điều đó chứng tỏ động lượng của hệ hai xe được bảo toàn. Định luật bảo toàn động lượng được nghiệm đúng.

III. Vận dụng định luật bảo toàn động lượng

Trong một hệ kín, nếu có một phần hệ chuyển động theo môt hướng, theo định luật bảo toàn động lượng, phần còn lại của hệ phải chuyển động theo hướng ngược lại. Chuyển động theo nguyên tắc như trên gọi là chuyển động bằng phản lực. Tên lửa là phương tiện hoạt động theo nguyên tắc đó cho thấy biểu hiện của định luật bảo toàn động lượng trong thực tiễn.