Đây là phiên bản do Nguyễn Phúc Đạt
đóng góp và sửa đổi vào 24 tháng 2 2023 lúc 15:59. Xem phiên bản hiện hành
Bài 1. Điểm. Đường thẳng
Nội dung lý thuyết
Các phiên bản khác
0
4 gp
I. ĐIỂM
- Dấu chấm nhỏ trên giấy là hình ảnh của điểm
- Ta dùng chữ cái in hoa A, B, C, D, ... để đặt tên cho điểm
Ví dụ. Ta có các điểm A, B, M, N, P dưới đây.
.png)
Trong hình trên, ta có các điểm A, B, N là các điểm phân biệt. Các điểm M, P là trùng nhau.
Quy ước: Khi nói hai điểm mà không nói gì thêm, ta hiểu đó là hai điểm phân biệt.
Chú ý: Mỗi hình là tập hợp các điểm. Hình có thể chỉ gồm một điểm.
II. ĐƯỜNG THẲNG
Chúng ta gặp rất nhiều hình ảnh đường thẳng trong đời sống. Chẳng hạn: mép bảng viết, mép cửa sổ, mép bàn, ...
|
|
- Đường thẳng không bị giới hạn về hai phía
- Ta dùng vạch thẳng để biểu diễn một đường thẳng
- Sử dụng những chữ cái in thường a, b, c, ... để đặt tên cho đường thẳng.
Ví dụ. Ta có đường thẳng a, b như hình dưới.
.png)
III. ĐIỂM THUỘC ĐƯỜNG THẲNG. ĐIỂM KHÔNG THUỘC ĐƯỜNG THẲNG
Trong hình vẽ bên, ta nói:
- Điểm A thuộc đường thẳng d, kí hiệu là A ∈ d.
- Điểm C thuộc đường thẳng d, kí hiệu là C ∉ d.
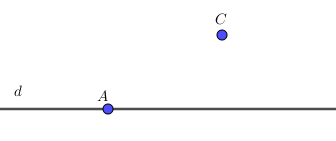
Điểm A thuộc đường thẳng d còn được gọi là điểm A nằm trên đường thẳng d hay đường thẳng d đi qua điểm A.
Điểm C không thuộc đường thẳng d còn được gọi là điểm C không nằm trên đường thẳng d hay đường thẳng d không đi qua điểm C.
Ví dụ. Trong hình dưới, những điểm nào thuộc đường thẳng a, những điểm nào không thuộc đường thẳng a? Sử dụng kí hiệu để ghi kết quả.

Giải:
- Điểm A và P thuộc đường thẳng a. Ta viết A ∈ a, P ∈ a.
- Điểm C và E không thuộc đường thẳng a. Ta viết C ∉ a, E ∉ a.
Chú ý: Có vô số điểm thuộc một đường thẳng.
IV. ĐƯỜNG THẲNG ĐI QUA HAI ĐIỂM

Đường thẳng đi qua hai điểm A, B còn được gọi là đường thẳng AB hay đường thẳng BA hay đường thẳng a.
Có một và chỉ một đường thẳng đi qua hai điểm A và B.
@582285@
V. BA ĐIỂM THẲNG HÀNG
- Khi ba điểm cùng thuộc một đường thẳng, ta nói chúng thẳng hàng.
- Khi ba điểm không cùng thuộc bất kì đường thẳng nào, ta nói chúng không thẳng hàng.
Chẳng hạn: Trong hình bên, ta có: 
- Ba điểm M, P, Q thẳng hàng.
- Ba điểm M, N, P hay M, N, Q hay P, Q, N không thẳng hàng.
Với ba điểm M, P, Q thẳng hàng, ta có:
- Hai điểm M, P nằm cùng phía đối với điểm Q.
- Hai điểm P, Q nằm cùng phía đối với điểm M.
- Hai điểm M, Q nằm khác phía đối với điểm P.
- Điểm P nằm giữa hai điểm M và Q.
Trong ba điểm thẳng hàng, có một và chỉ một điểm nằm giữa hai điểm còn lại.
@582367@
Danh sách các phiên bản khác của bài học này. Xem hướng dẫn
| Nguyễn Phúc Đạt đã đóng góp một phiên bản khác cho bài học này (24 tháng 2 2023 lúc 15:59) | 0 lượt thích |

