§4. Bất phương trình bậc nhất hai ẩn
Nội dung lý thuyết
Các phiên bản khácI. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Bất phương trình bậc nhất hai ẩn \(x,y\) có dạng tổng quát là \(ax+by\le c\) (1)
(\(ax+by< c;ax+by\ge c;ax+by>c\))
trong đó \(a,b,c\) là những số thực đã cho, \(a\) và \(b\) không đồng thời bằng \(0\), \(x\) và \(y\) là các ẩn số.
Ví dụ: +) \(3x-2y\le-1\) là một bất phương trình bậc nhất hai ẩn \(x,y\).
Ta có thể kể đến một vài cặp số là nghiệm của bất phương trình này như: \(\left(x;y\right)=\left(-1;2\right)\), \(\left(x;y\right)=\left(\dfrac{3}{2};3\right)\); \(\left(x;y\right)=\left(-4;-\dfrac{5}{2}\right)\) ; ...
+) \(\dfrac{1}{2}x-\dfrac{7}{3}y>2\) là một bất phương trình bậc nhất hai ẩn \(x,y\).
Ta có thể kể đến một vài cặp số là nghiệm của bất phương trình này như: \(\left(x;y\right)=\left(1;-1\right)\) ; \(\left(x;y\right)=\left(-2;-3\right)\) , ...
@1892871@
II. BIỂU DIỄN TẬP NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Cũng như bất phương trình bậc nhất một ẩn, các bất phương trình bậc nhất hai ẩn thường có vô số nghiệm và để mô tả tập nghiệm của chúng, ta sử dụng phương pháp biểu diễn hình học.
Trong mặt phẳng toạ độ \(Oxy\), tập hợp các điểm có toạ độ là nghiệm bất phương trình (1) được gọi là miền nghiệm của nó.
Người ta đã chứng minh được rằng trong mặt phẳng toạ độ \(Oxy\), đường thẳng \(ax+by=c\) chia mặt phẳng thành hai nửa mặt phẳng, một trong hai nửa mặt phẳng đó là miền nghiệm của bất phương trình \(ax+by\le c\), nửa mặt phăng còn lại là miền nghiệm của bất phương trình \(ax+by\ge c\).
Từ đó ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình \(ax+by\le c\) như sau (tương tự cho bất phương trình \(ax+by\ge c\)):
Bước 1: Trên mặt phẳng toạ độ \(Oxy\), vẽ đường thẳng \(\Delta\): \(ax+by=c\)
Bước 2: Lấy một điểm \(M_0\left(x_0;y_0\right)\) không thuộc đường thẳng \(\Delta\): \(ax+by=c\) (ta thường lấy gốc toạ độ \(O\))
Bước 3: Tính \(ax_0+by_0\) và so sánh \(ax_0+by_0\) với \(c\)
Bước 4: Kết luận:
Nếu \(ax_0+by_0< c\) thì nửa mặt phẳng bờ \(\Delta\) chứa \(M_0\) là miền nghiệm của bất phương trình \(ax+by\le c\);
Nếu \(ax_0+by_0>c\) thì nửa mặt phẳng bờ \(\Delta\) chứa \(M_0\) là miền nghiệm của bất phương trình \(ax+by\ge c\).
Chú ý: Miền nghiệm của bất phương trình \(ax+by\le c\) bỏ đi đường thẳng \(ax+by=c\) là miền nghiệm của bất phương trình \(ax_0+by_0< c\).
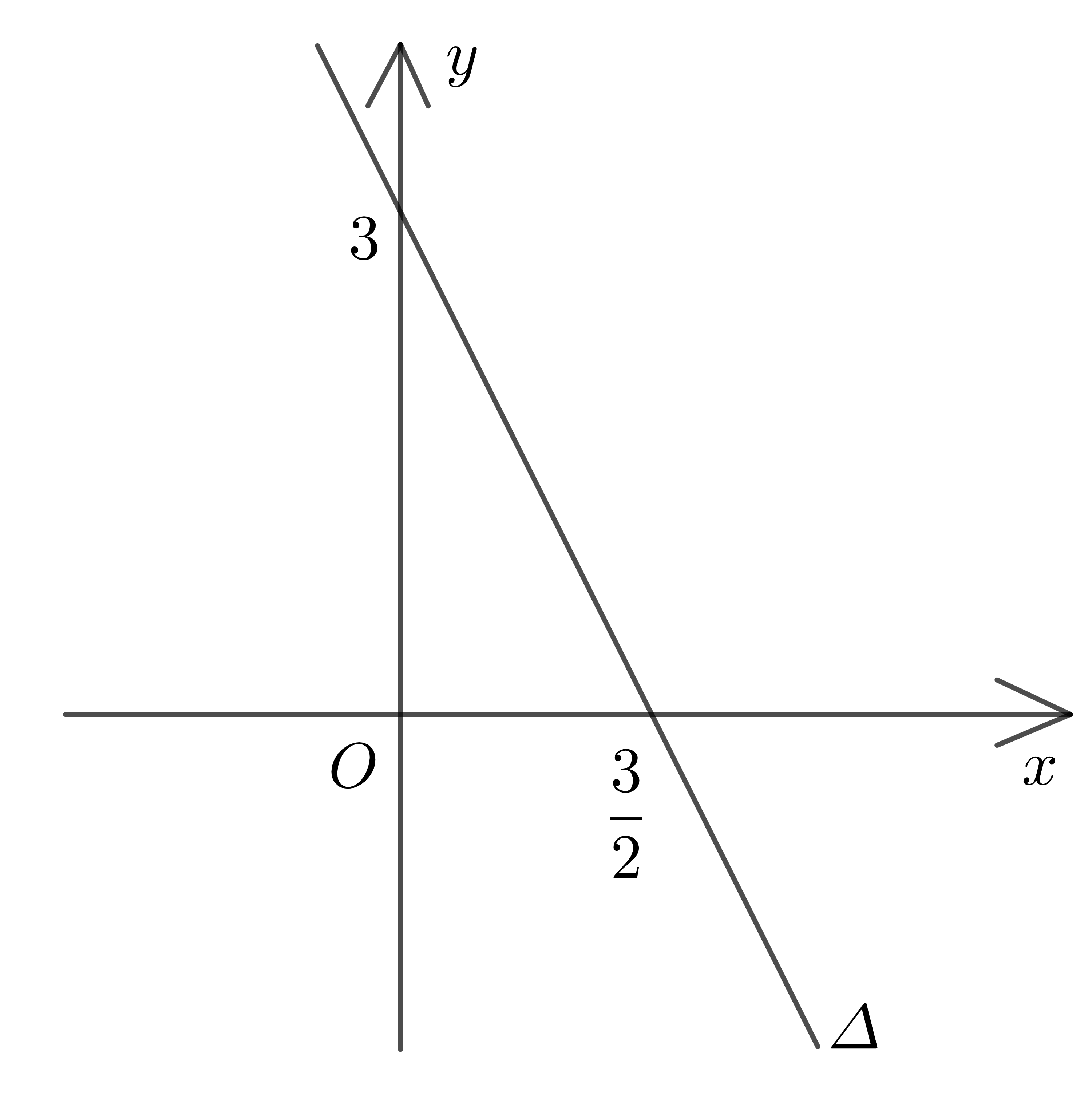
Ví dụ 1: Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn \(2x+y\le3\).
Giải:
Vẽ đường thẳng \(\Delta\):\(2x+y=3\)
Lấy gốc toạ độ \(O\left(0;0\right)\), ta thấy \(O\notin\Delta\) và có \(2.0+0=0< 3\) nên nửa mặt phẳng bờ \(\Delta\) có chứa \(O\) là miền nghiệm của bất phương trình đã cho.
@1892428@
III. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn \(x,y\) mà ta phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho.
Cũng như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn.
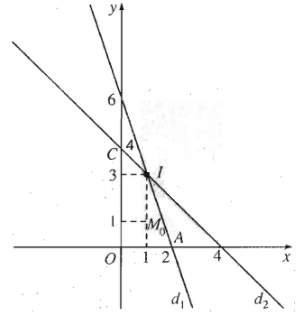
Ví dụ 2: Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn \(\left\{{}\begin{matrix}3x+y\le6\\x+y\le4\\x\ge0\\y\ge0\end{matrix}\right.\)
Giải:
Vẽ các đường thẳng: \(\left(d_1\right)3x+y=6\)
\(\left(d_2\right)x+y=4\)
\(\left(d_3\right)x=0\) (trục hoành)
\(\left(d_4\right)y=0\) (trục tung)
Vì điểm \(M_0\left(1;1\right)\) có toạ độ thoả mãn tất cả các bất phương trình trong hệ trên nên ta loại các điểm thuộc các nửa mặt phẳng bờ \(\left(d_1\right),\left(d_2\right),\left(d_3\right),\left(d_4\right)\) không chứa điểm \(M_0\left(1;1\right)\). Miền không tô đậm (tứ giác \(OCIA\) kể cả 4 cạnh \(OC,CI,IA,AO\)) là miền nghiệm của hệ bất phương trình.
@1892345@
IV. ÁP DỤNG VÀO BÀI TOÁN KINH TẾ
Giải một số bài toán kinh tế thường dẫn đến việc xét những hệ bất phương trình bậc nhất hai ẩn và giải chúng. Loại bài toán này được nghiên cứu trong một ngành toán học có tên gọi Quy hoạch tuyến tính. Ta sẽ xét một bài toán đơn giản thuộc loại đó.
Bài toán: Một phân xưởng có hai máy đặc chủng \(M_1,M_2\) sản xuất hai loại sản phẩm kí hiệu là \(I\) và \(II\). Một tấn sản phẩm loại \(I\) lãi 2 triệu đồng, một tấn sản phẩm loại \(II\) lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại \(I\) phải dùng máy \(M_1\) trong 3 giờ và máy \(M_2\) trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại \(II\) phải dùng máy \(M_1\) trong 1 giờ và máy \(M_2\) trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy \(M_1\) làm việc không quá 6 giờ trong một ngày, máy \(M_2\) làm việc không quá \(4\) giờ trong một ngày. Hãy đặt kế hoạch sản xuất sao cho tổng số tiền lãi cao nhất.
Giải:
Gọi \(x,y\) theo thứ tự là số sản phẩm loại \(I\), loại \(II\) sản xuất trong 1 ngày (\(x\ge0,y\ge0\))
Như vậy tiền lãi mỗi ngày là \(L=2x+1,6y\) (triệu đồng) và số giờ làm việc (mỗi ngày) của máy \(M_1\) là \(3x+y\) (giờ) và của máy \(M_2\) là \(x+y\) (giờ).
Vì mỗi ngày máy \(M_1\) không làm việc quá 6 giờ nên ta có \(3x+y\le6\), máy \(M_2\) làm việc không quá 4 giờ nên ta có \(x+y\le4\)
Như vậy \(x,y\) phải thoả mãn hệ bất phương trình: \(\left\{{}\begin{matrix}3x+y\le6\\x+y\le4\\x\ge0\\y\ge0\end{matrix}\right.\) (2)
Bài toán trở thành: Trong các nghiệm của bất phương trình (2), tìm nghiệm \(\left(x=x_0;y=y_0\right)\) sao cho \(L=2x+1,6y\) đạt giá trị lớn nhất.
Miền nghiệm của hệ (2) là tứ giác \(OCIA\) kể cả miền trong (gọi là miền tứ giác \(OCIA\)) ở ví dụ trên.
Người ta chứng minh được rằng biểu thức \(L=2x+1,6y\) đạt giá trị lớn nhất tại một trong các đỉnh của tứ giác \(OCIA\). Tính giá trị của biểu thức \(L=2x+1,6y\) tại tất cả các đỉnh của tứ giác \(OCIA\), ta thấy \(L\) lớn nhất tại \(x=1,y=3\).
Vậy để số tiền lãi cao nhất, mỗi ngày cần sản xuất 1 tấn sản phẩm loại \(I\) và 3 tấn sản phẩm loại \(II\).