§2. Tập hợp
Nội dung lý thuyết
Các phiên bản khácI. KHÁI NIỆM TẬP HỢP
1. Tập hợp và phần tử
Tập hợp (còn gọi là tập) là một khái niệm cơ bản của toán học, không định nghĩa.
Giả sử đã cho tập hợp \(A\). Để chỉ \(a\) là một phần tử của tập hợp \(A\), ta viết \(a\in A\) (đọc là \(a\)thuộc \(A\)). Để chỉ \(a\) không phải là một phần tử của tập hợp \(A\), ta viết \(a\notin A\) (đọc là \(a\) không thuộc \(A\)).
Ví dụ:
+) Để chỉ \(5\) là một số tự nhiên, ta viết: \(5\in N\) ;
+) Để chỉ \(\sqrt{2}\) không phải là một số hữu tỉ, ta viết: \(\sqrt{2}\notin Q\) ;
+) Để chỉ \(4\) là một ước của \(20\), ta viết: \(4\inƯ\left(20\right)\).
@70191@
2. Cách xác định tập hợp
Ta có thể xác định một tập hợp bằng một trong hai cách:
a) Liệt kê các phần tử của nó ;
b) Chỉ ra tính chất đặc trưng cho các phần tử của nó.
Ví dụ 1: Tập hợp \(A\) bao gồm các số tự nhiên nhỏ hơn \(10\) và chia hết cho \(5\). Ta có thể biểu diễn tập hợp \(A\) như sau:
+) Cách 1: Liệt kê các phần tử của \(A\): \(A=\left\{0;5;10\right\}\);
+) Cách 2: Chỉ ra tính chất đặc trưng của các phần tử của \(A\): \(A=\left\{x\in N|x< 10;x⋮5\right\}\)
Ví dụ 2: Tập hợp \(B\) bao gồm các phần tử là nghiệm của phương trình \(x^2-3x+2=0\). Ta thấy phương trình trên có hai nghiệm phân biệt là \(x=1,x=2\). Ta có thể biểu diễn tập hợp \(B\) như sau:
+) Cách 1: \(B=\left\{1;2\right\}\) ;
+) Cách 2: \(B=\left\{x\in R|x^2-3x+2=0\right\}\).
Ngoài ra, người ta còn có thể biểu diễn tập hợp bằng một hình phẳng được bao quanh bởi một đường kín, gọi là biểu đồ Ven, như sau:

@70198@
3. Tập hợp rỗng
Tập hợp rỗng, kí hiệu là \(\varnothing\), là tập hợp không chứa phần tử nào.
Ví dụ: Tập hợp \(A\) bao gồm các phần tử là nghiệm của phương trình \(x^2+x+1=0\).
Ta thấy: \(x^2+x+1\) là một bình phương thiếu \(\Rightarrow\) \(x^2+x+1>0,\forall x\)
Nên phương trình \(x^2+x+1=0\) là phương trình vô nghiệm.
Do đó tập hợp \(A\) không có phần tử nào.
Ta gọi \(A\) là một tập hợp rỗng, kí hiệu là \(A=\varnothing\).
Nếu \(A\) không phải là tập hợp rỗng thì \(A\) chứa ít nhất một phần tử.
\(A\ne\varnothing\Leftrightarrow\exists x:x\in A\)
@70217@
II. TẬP HỢP CON
Nếu mọi phần tử của tập hợp \(A\) đều là phần tử của tập hợp \(B\) thì ta nói \(A\) là một tập hợp con của \(B\) và được kí hiệu là \(A\subset B\) (đọc là \(A\) chứa trong \(B\)).
Thay cho \(A\subset B\), ta cũng có thể viết \(B\supset A\) (đọc là \(B\) chứa \(A\) hay \(B\) bao hàm \(A\)).
Như vậy \(A\subset B\Leftrightarrow\left(\forall x:x\in A\Rightarrow x\in B\right)\).
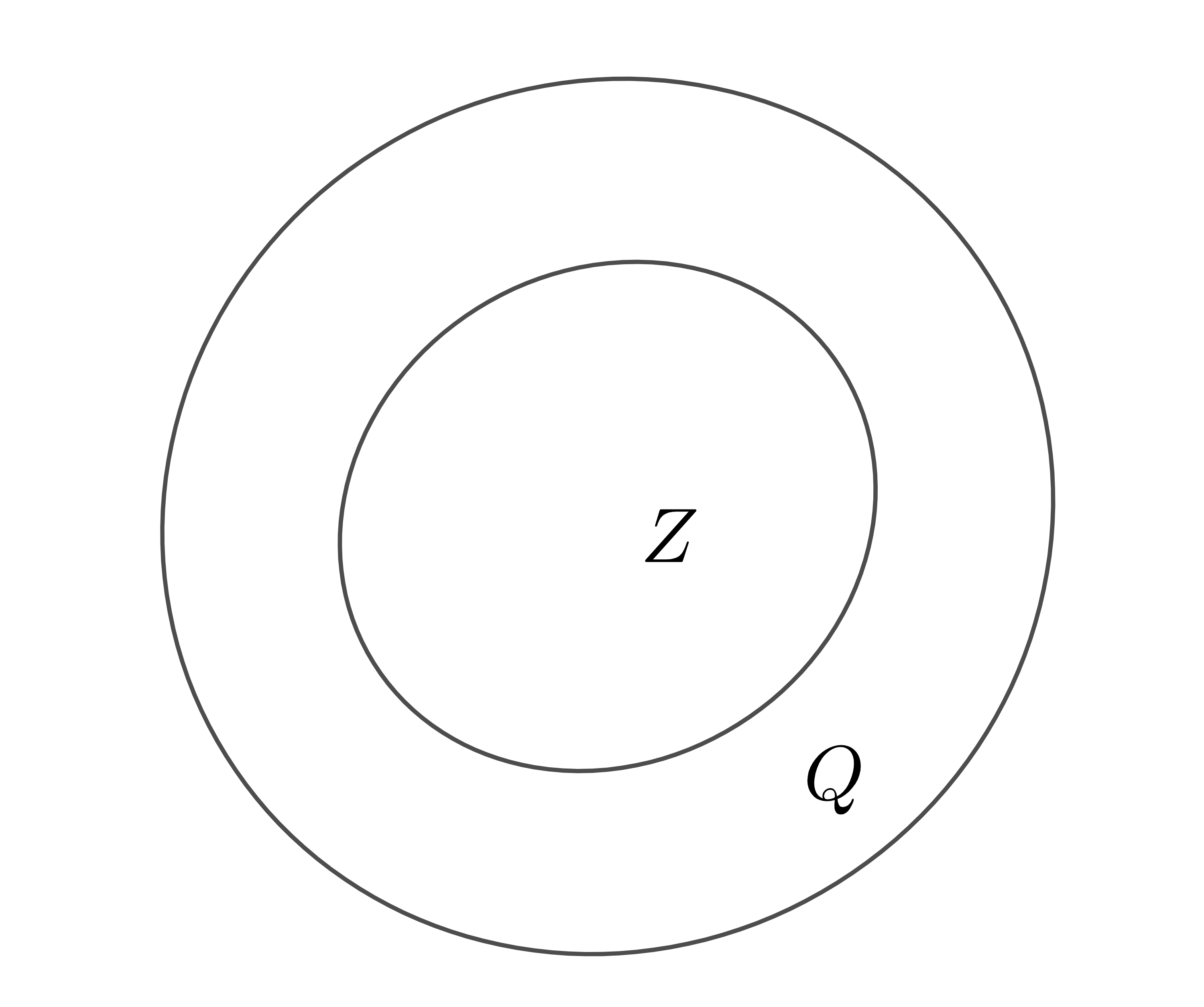
Ví dụ 1: Xét tập số nguyên \(Z\) và tập số hữu tỉ \(Q\).
Ta nhận thấy tất cả các số nguyên đều là số hữu tỉ, do đó mọi phần tử của tập hợp \(Z\) đều là phần tử của tập hợp \(Q\).
Ta nói \(Z\) là tập hợp con của \(Q\) và kí hiệu là \(Z\subset Q\).
Ta cũng có thể biểu diễn bằng biểu đồ Ven như sau:
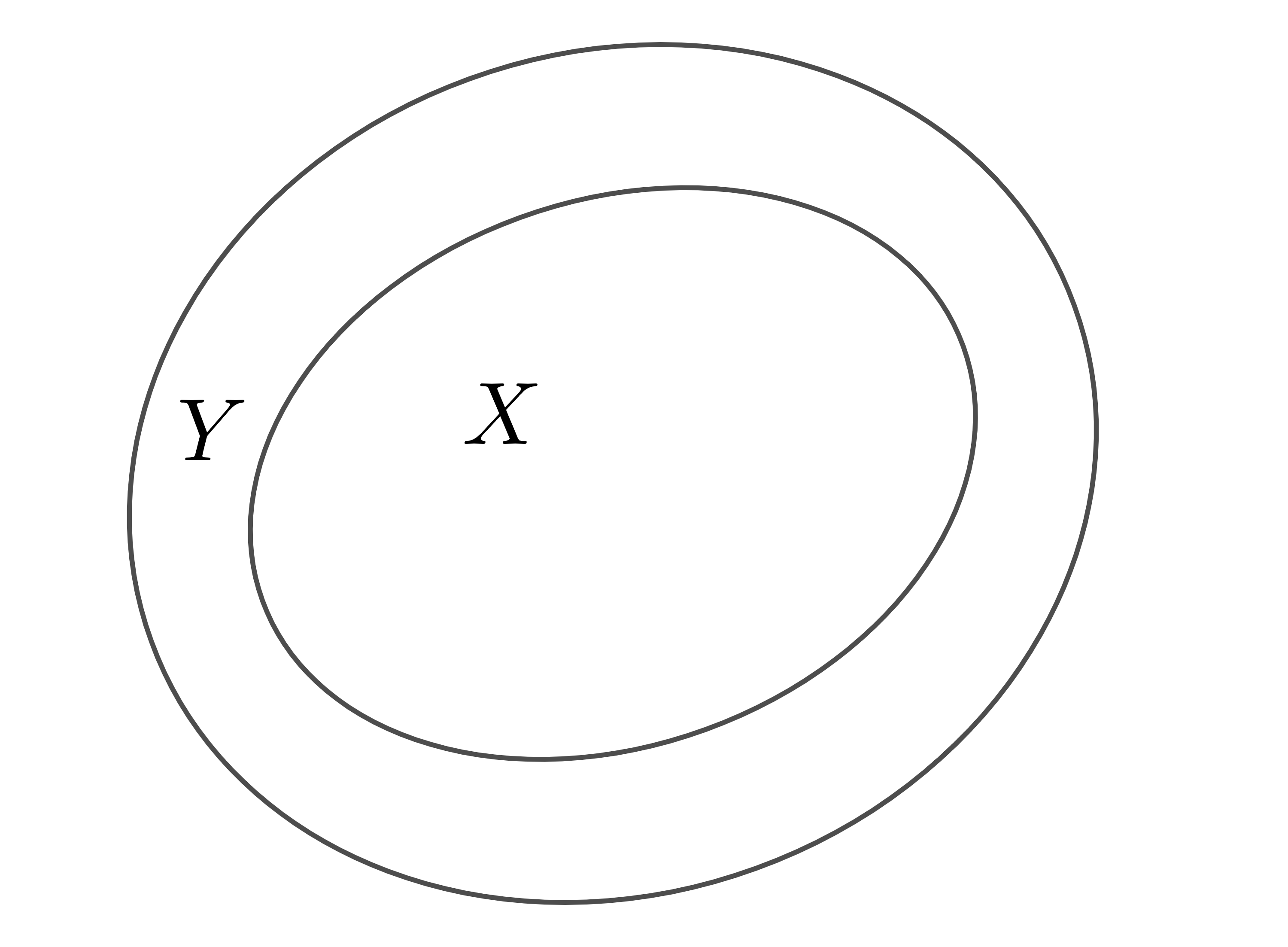
Ví dụ 2: Xét tập hợp \(X=\left\{1;2;3\right\}\) và tập hợp \(Y=\left\{1;2;3;4;5\right\}\)
Ta nói: \(X\subset Y\) hay \(Y\supset X\).
Biểu đồ Ven:
Ví dụ 3: Xét tập hợp \(M=\left\{x\in N|x^2-1=0\right\}\) và tập hợp \(N=\left\{x\in Z|x^2-8x+7=0\right\}\)
Ta có thể biểu diễn hai tập hợp trên bằng cách liệt kê các phần tử của chúng như sau:
\(M=\left\{1\right\}\)
\(N=\left\{1;7\right\}\)
Ta nói \(M\subset N\) (\(M\) là tập hợp con của \(N\)) hay \(N\supset M\) (\(N\) bao hàm \(M\)).
Nếu \(A\) không phải là tập hợp con của \(B\), ta viết
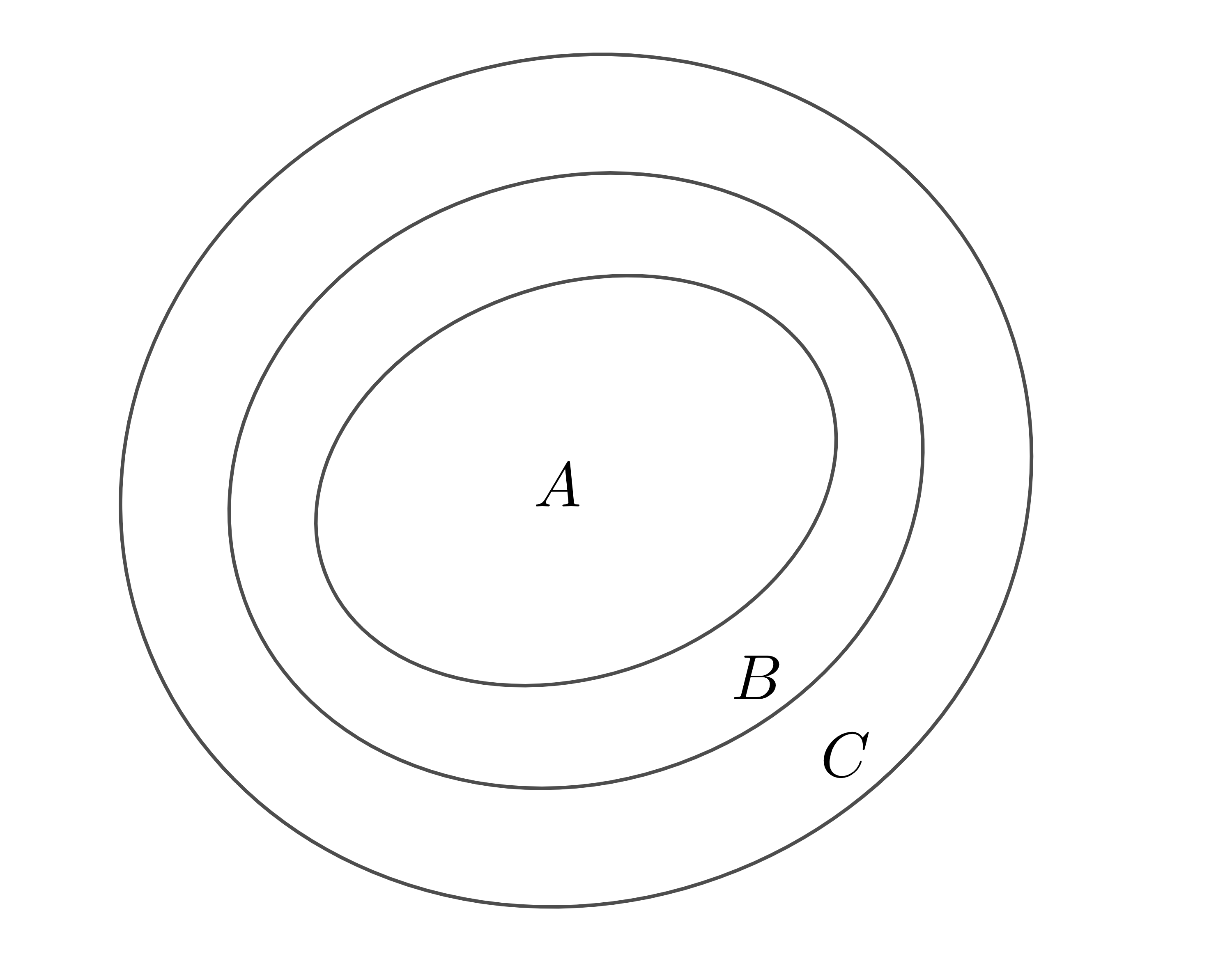
Ta có tính chất:
a) \(A\subset A\) với mọi tập hợp \(A\) ;
b) Nếu \(A\subset B\) và \(B\subset C\) thì \(A\subset C\) ;
c) \(\varnothing\subset A\) với mọi tập hợp \(A\).
@70196@
III. TẬP HỢP BẰNG NHAU
Khi \(A\subset B\) và \(B\subset A\) ta nói tập hợp \(A\) bằng tập hợp \(B\) và kí hiệu là \(A=B\).
Như vậy: \(A=B\Leftrightarrow\left(\forall x:x\in A\Leftrightarrow x\in B\right)\).
Ví dụ: Xét 2 tập hợp:
\(A=\left\{x\in N|x< 10;x⋮3\right\}\)
\(B=\left\{0;3;6;9\right\}\)
Ta có thể viết tập hợp \(A=\left\{0;3;6;9\right\}\)
Từ đó suy ra \(A=B\).