Ai biết giải giúp mik vs ạ, biết câu nào giải câu đó cx đc ko cần giải hết, mik xin cảm ơn❤️
Bài 9. Định luật Ôm đối với toàn mạch
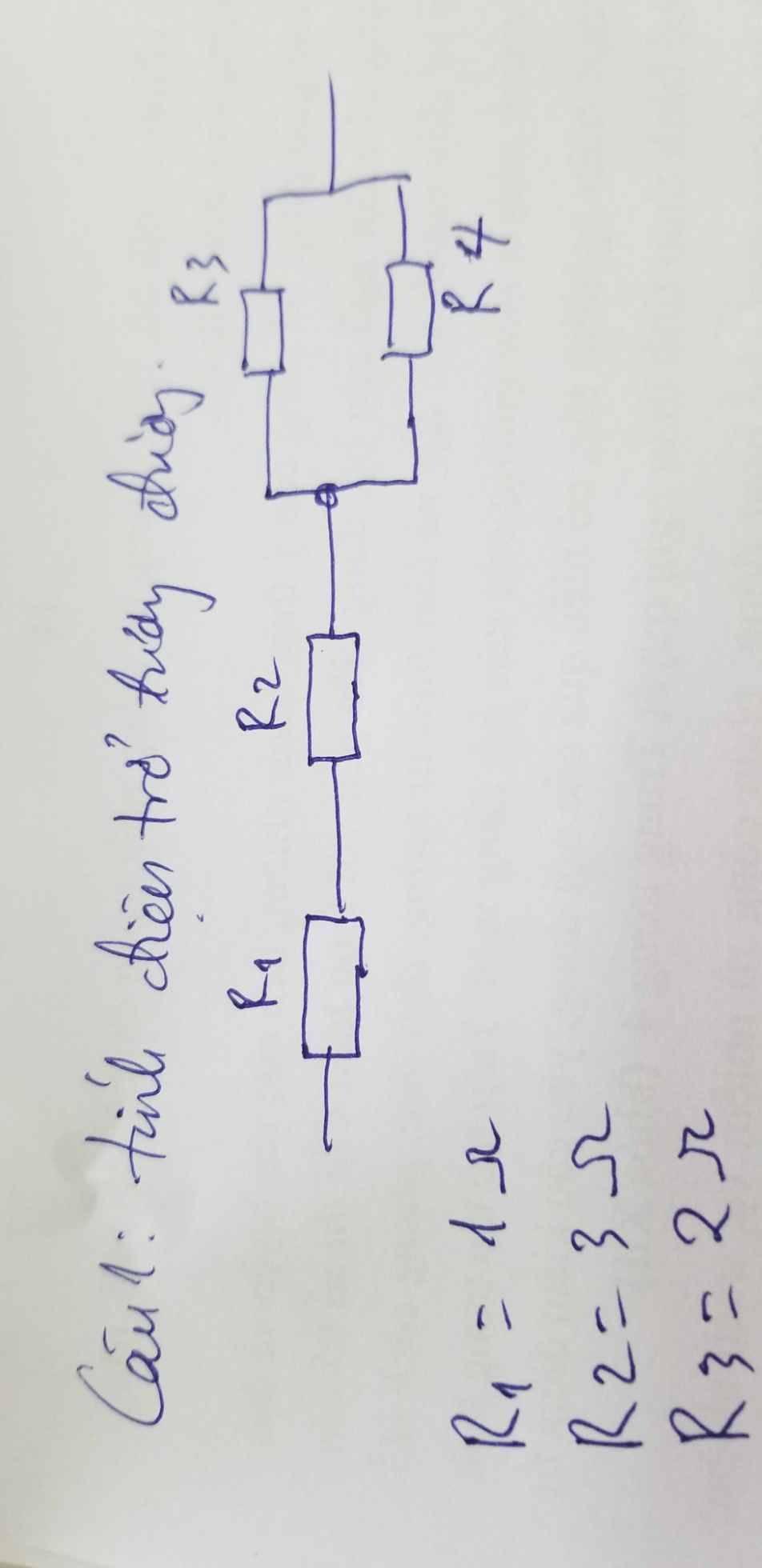
Phải dùng tối thiểu bảo nhiêu điện trở loại 3 ôm để mắc thành điện trở có điện trở là 4 ôm.
Để \(R_{td}=4\Omega\Rightarrow MCD:R_1nt\left(R_2//R_3//R_4\right)\)
Ta có: \(\dfrac{1}{R_{234}}=\dfrac{1}{R_2}+\dfrac{1}{R_3}+\dfrac{1}{R_4}=\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}=1\)
\(\rightarrow R_{234}=1\Omega\)
\(\Rightarrow R_{td}=R_1+R_{234}=3+1=4\Omega\left(tmycdb\right)\)
Đúng 1
Bình luận (0)
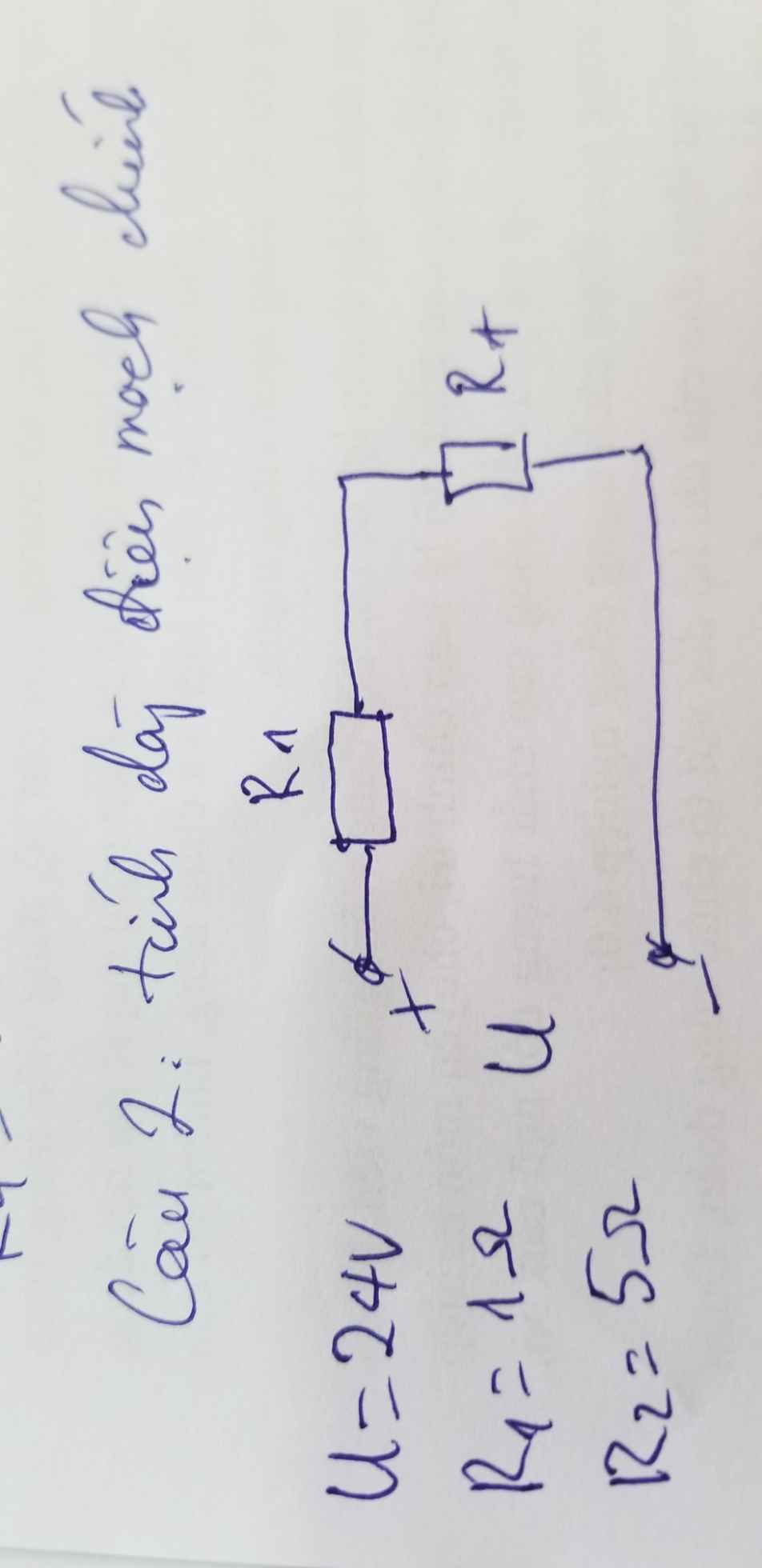
Câu 2.
\(R_1ntR_2\Rightarrow R_{tđ}=R_1+R_2=1+5=6\Omega\)
Dòng điện qua mạch chính:
\(I_{mạch}=\dfrac{U}{R_{tđ}}=\dfrac{24}{6}=4A\)
Đúng 1
Bình luận (0)
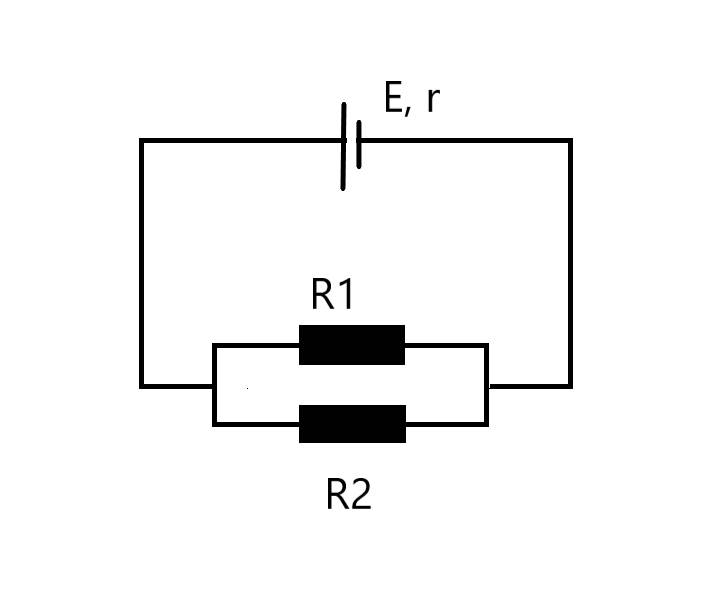
Có mạch điện như hình vẽ. Nguồn điện có suất điện động E=12V, điện trở trong r=3 ôm. Điện trở R1=12 ôm. Hỏi R2 bằng bao nhiêu để: a) Công suất mạch ngoài lớn nhất. Tính công suất này. b) Công suất trên R2 lớn nhất. Tính cường độ dòng điện trong mạch khi đó.
Nguồn điện (E, r) thắp sáng bình thường 4 bóng đènloại (6V- 3W) kể cả khi chúng được mắc song song hay mắc nối tiếp vào hai cực của nguồn.a. Tính điện trở và cường độ dòng điện định mức của mỗi đèn.b. Tính cường độ dòng điện qua nguồn khi các đèn được mắc song song và khi được mắcnối tiếp vào nguồn.c. Tính E và r.d. Với nguồn này có thể thắp sáng bình thường tốiđa bao nhiêu đèn (6V- 3W)
Đọc tiếp
Nguồn điện (E, r) thắp sáng bình thường 4 bóng đèn
loại (6V- 3W) kể cả khi chúng được mắc song song hay mắc nối tiếp vào hai cực của nguồn.
a. Tính điện trở và cường độ dòng điện định mức của mỗi đèn.
b. Tính cường độ dòng điện qua nguồn khi các đèn được mắc song song và khi được mắc
nối tiếp vào nguồn.
c. Tính E và r.
d. Với nguồn này có thể thắp sáng bình thường tối
đa bao nhiêu đèn (6V- 3W)
Khi mắc điện trở R1 = 10 ôm vào hai cực của một nguồn điện thì dòng điện chạy trong mạch là 2A, khi nối mắc điện trở R2 = 14 ôm vào hai cực của một nguồn điện thì dòng điện chạy trong mạch là 1,5A. Tính suất điện động và điện trở trong của nguồn điện.
Ta có
\(E=I_1\left(R_1+r\right)=I_2\left(R_2+r\right)\\ \Leftrightarrow2\left(10+r\right)=1,5\left(14+r\right)\Rightarrow r=2\\ \Rightarrow E=2\left(10+2\right)=24\)
Đúng 2
Bình luận (0)
Giúp em với ạ em cảm ơn
CTM: \(\left[R_3nt\left(R_1//\left(R_2ntR_4\right)\right)\right]\)
\(R_{24}=2+2=4\Omega\)
\(R_{124}=\dfrac{R_1\cdot R_{24}}{R_1+R_{24}}=\dfrac{2\cdot4}{2+4}=\dfrac{4}{3}\Omega\)
\(R_{tđ}=R_3+R_{124}=2+\dfrac{4}{3}=\dfrac{10}{3}\Omega\)
\(R_{mạch}=R_{tđ}+r=\dfrac{10}{3}+1=\dfrac{13}{3}\Omega\)
\(I_A=I_{mạch}=\dfrac{\xi}{R_{mạch}}=\dfrac{6,9}{\dfrac{13}{3}}=1,59A\)
Đúng 3
Bình luận (0)
Đặt 1 dây dẫn thẳng dài vô hạn thứ 2 mang dòng điện I2 = 5A cách dây dẫn mang dòng điện một khoảng 10 cm. Tính cảm ứng từ tại điểm M nằm trên đường nối 2 dây dẫn và cách đều 2 dây dẫn?
\(B_1=B_2=2\cdot10^{-7}\cdot\dfrac{I}{r}=2\cdot10^{-7}\cdot\dfrac{5}{0,1}=10^{-5}T\)
Tại M có cảm ứng từ.
Do M cách đều hai dây dẫn nên:
\(B_M=B_1=B_2=10^{-5}T\)
Đúng 4
Bình luận (0)
Cho mạch điện như hình vẽ. Năm bóng đèn trong mạch giống hệt nhau. U không đổi. Ban đầu cả hai khóa đều đóng.
a. Hãy sắp các bóng đèn theo thứ tự độ sáng tăng dần.
b. Trạng thái hai khóa như thế nào để đèn 4 có độ sáng nhỏ nhất có thể.
Giúp mk với ạ ☺️
Khi k mở, dòng điện chỉ chạy qua R1
Ta có: \(I=\dfrac{\varepsilon}{R+r}\Leftrightarrow2=\dfrac{6}{2+r}\Rightarrow r=1\Omega\)
Khi k đóng, mạch điện có sơ đồ: R1//R
Ta có, công suất tiêu thu trên R là: \(P=UI=I^2R\) (*)
Lại có: \(I=\dfrac{\varepsilon}{r+\dfrac{RR_1}{R+R_1}}\)
Thay I vào (*) ta có: \(P=\left(\dfrac{\varepsilon}{r+\dfrac{RR_1}{R+R_1}}\right)^2R=\dfrac{\varepsilon^2}{\left(\dfrac{r}{\sqrt{R}}+\dfrac{RR_1}{\sqrt{R}\left(R+R_1\right)}\right)}\)
\(P=\dfrac{\varepsilon^2}{\left(\dfrac{r}{\sqrt{R}}+\dfrac{RR_1}{\sqrt{R}\left(R+R_1\right)}\right)}=\dfrac{\varepsilon^2}{\left(\dfrac{r}{\sqrt{R}}+\dfrac{R_1\sqrt{R}}{\left(R+R_1\right)}\right)}\)
Để P cực đại thì mẫu số của nó phải đạt GTNN
Áp dụng bất đẳng thức Cosi vào 2 số \(\dfrac{r}{\sqrt{R}}\) và \(\dfrac{\sqrt{R}R_1}{\left(R+R_1\right)}\), ta có:
\(\dfrac{r}{\sqrt{R}}+\dfrac{\sqrt{R}R_1}{\left(R+R_1\right)}\ge2\sqrt{\dfrac{rR_1}{\left(R+R_1\right)}}\)
\(\dfrac{r}{\sqrt{R}}+\dfrac{R_1\sqrt{R}}{\left(R+R_1\right)}\) đạt giá trị nhỏ nhất khi \(\dfrac{r}{\sqrt{R}}=\dfrac{\sqrt{R}R_1}{\left(R+R_1\right)}\)
\(\Rightarrow r\left(R+R_1\right)=RR_1\Leftrightarrow1\left(R+2\right)=2R\Rightarrow R=2\Omega\)
Khi đó P=18W
Đúng 2
Bình luận (0)