Rút gọn biểu thức \({\left[ {{{\left( {\frac{1}{3}} \right)}^2}} \right]^{\frac{1}{4}}}.{\left( {\sqrt 3 } \right)^5}\), ta được
A. \(\sqrt 3 \).
B. \(3\sqrt 3 \).
C. \(\frac{1}{{\sqrt 3 }}\).
D. 9.
Rút gọn biểu thức \({\left[ {{{\left( {\frac{1}{3}} \right)}^2}} \right]^{\frac{1}{4}}}.{\left( {\sqrt 3 } \right)^5}\), ta được
A. \(\sqrt 3 \).
B. \(3\sqrt 3 \).
C. \(\frac{1}{{\sqrt 3 }}\).
D. 9.
Nếu \({2^\alpha } = 9\) thì \({\left( {\frac{1}{{16}}} \right)^{\frac{\alpha }{8}}}\) có giá trị bằng
A. \(\frac{1}{3}\).
B. 3.
C. \(\frac{1}{9}\).
D. \(\frac{1}{{\sqrt 3 }}\).
\({\left( {\frac{1}{{16}}} \right)^{\frac{\alpha }{8}}} = {\left( {{2^{ - 4}}} \right)^{\frac{\alpha }{8}}} = {2^{ - 4.\frac{\alpha }{8}}} = {2^{ - \frac{1}{2}\alpha }} = {\left( {{2^\alpha }} \right)^{ - \frac{1}{2}}} = {9^{ - \frac{1}{2}}} = \frac{1}{3}\)
Chọn A.
Trả lời bởi Hà Quang MinhNếu \({a^{\frac{1}{2}}} = b\left( {a > 0,a \ne 1} \right)\) thì
A. \({\log _{\frac{1}{2}}}a = b\).
B. \(2{\log _a}b = 1\).
C. \({\log _a}\frac{1}{2} = b\).
D. \({\log _{\frac{1}{2}}}b = a\).
\({a^{\frac{1}{2}}} = b \Leftrightarrow {\log _a}b = \frac{1}{2} \Leftrightarrow 2{\log _a}b = 1\)
Chọn B.
Trả lời bởi Hà Quang MinhNếu \(x = {\log _3}4 + {\log _9}4\) thì \({3^x}\) có giá trị bằng
A. 6.
B. 8.
C. 16.
D. 64.
\(x=log_34+log_94\\ =log_34+\dfrac{1}{2}log_34\\ =log_34+log_32\\ =log_38\\ \Leftrightarrow3^x=8\)
Chọn B.
Trả lời bởi Hà Quang MinhCho \(\alpha ,\beta \) là hai số thực với \(\alpha < \beta \). Khẳng định nào sau đây đúng?
A. \({\left( {0,3} \right)^\alpha } < {\left( {0,3} \right)^\beta }\).
B. \({\pi ^\alpha } \ge {\pi ^\beta }\).
C. \({\left( {\sqrt 2 } \right)^\alpha } < {\left( {\sqrt 2 } \right)^\beta }\).
D. \({\left( {\frac{1}{2}} \right)^\beta } > {\left( {\frac{1}{2}} \right)^\alpha }\).
Ta có:
A. \(\alpha< \beta\)
\(\Rightarrow\left(0,3\right)^{\alpha}>\left(0,3\right)^{\beta}\)
Sai
B. \(\alpha< \beta\)
\(\Rightarrow\pi^{\alpha}< \pi^{\beta}\)
Sai
C. \(\alpha< \beta\)
\(\Rightarrow\left(\sqrt{2}\right)^{\alpha}< \left(\sqrt{2}\right)^{\beta}\)
Đúng
D. \(\alpha< \beta\)
\(\Rightarrow\left(\dfrac{1}{2}\right)^{\alpha}>\left(\dfrac{1}{2}\right)^{\beta}\)
Sai
⇒ Chọn C
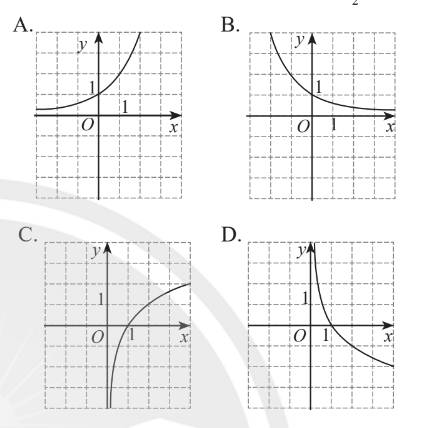
Trả lời bởi HT.Phong (9A5)Hình nào vẽ đồ thị của hàm số \(y = {\log _{\frac{1}{2}}}x\)?
Phương trình \(0,{1^{2{\rm{x}} - 1}} = 100\) có nghiệm là:
A. \( - \frac{1}{2}\).
B. \(\frac{1}{3}\).
C. \(1\frac{1}{2}\).
D. \(2\frac{1}{3}\).
\(0,1^{2x-1}=100\)
\(\Leftrightarrow0,1^{2x-1}=0,1^{log_{0,1}100}\)
\(\Leftrightarrow2x-1=log_{0,1}100\)
\(\Leftrightarrow2x-1=-2\)
\(\Leftrightarrow2x=-1\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
Chọn A
Trả lời bởi HT.Phong (9A5)Tập nghiệm của bất phương trình \(0,{5^{3{\rm{x}} - 1}} > 0,25\) là
A. \(\left( { - \infty ;1} \right)\).
B. \(\left( {1; + \infty } \right)\).
C. \(\left( {0;1} \right)\).
D. \(\left( { - \infty ; - \frac{1}{3}} \right)\).
\(0,5^{3x-1}>0,25\)
\(\Leftrightarrow0,5^{3x-1}>0,5^2\)
\(\Leftrightarrow3x-1< 2\)
\(\Leftrightarrow3x< 3\)
\(\Leftrightarrow x< \dfrac{3}{3}\)
\(\Leftrightarrow x< 1\)
Vậy: \(\left(-\infty;1\right)\)
Chọn A
Trả lời bởi HT.Phong (9A5)Nếu \(\log x = 2\log 5 - \log 2\) thì
A. \(x = 8\).
B. \(x = 23\).
C. \(x = 12,5\).
D. \(x = 5\).
ĐK: \(x>0\)
\(logx=2log5-log2\\ \Leftrightarrow logx=log25-log2\\ \Leftrightarrow logx=log\dfrac{25}{2}\Leftrightarrow x=12,5\)
Chọn C.
Trả lời bởi Hà Quang MinhSố nguyên \(x\) nhỏ nhất thoả mãn \({\log _{0,1}}\left( {1 - 2x} \right) > - 1\) là
A. \(x = 0\).
B. \(x = 1\).
C. \(x = - 5\).
D. \(x = - 4\).
ĐK: \(1-2x>0\Leftrightarrow x< \dfrac{1}{2}\)
\(log_{0,1}\left(1-2x\right)>-1\\ \Leftrightarrow1-2x< 10\\ \Leftrightarrow2x>-9\\ \Leftrightarrow x>-\dfrac{9}{2}\)
Kết hợp với ĐKXĐ, ta được: \(-\dfrac{9}{2}< x< \dfrac{1}{2}\)
Vậy số nguyên x nhỏ nhất thỏa mãn \(log_{0,1}\left(1-2x\right)>-1\) là \(x=-4\)
Chọn D.
Trả lời bởi Hà Quang Minh
\({\left[ {{{\left( {\frac{1}{3}} \right)}^2}} \right]^{\frac{1}{4}}}.{\left( {\sqrt 3 } \right)^5} = {\left( {\frac{1}{3}} \right)^{2.\frac{1}{4}}}.{\left( {{3^{\frac{1}{2}}}} \right)^5} = {\left( {{3^{ - 1}}} \right)^{\frac{1}{2}}}{.3^{\frac{1}{2}.5}} = {3^{ - \frac{1}{2}}}{.3^{\frac{5}{2}}} = {3^{ - \frac{1}{2} + \frac{5}{2}}} = {3^2} = 9\)
Chọn D.
Trả lời bởi Hà Quang Minh