Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng (a; b). Phát biểu nào dưới đây là đúng?
A. Nếu \(f'\left( x \right) \ge 0\) với mọi x thuộc (a; b) thì hàm số \(y = f\left( x \right)\) đồng biến trên (a; b).
B. Nếu \(f'\left( x \right) > 0\) với mọi x thuộc (a; b) thì hàm số \(y = f\left( x \right)\) đồng biến trên (a; b).
C. Hàm số \(y = f\left( x \right)\) đồng biến trên (a; b) khi và chỉ khi \(f'\left( x \right) \ge 0\) với mọi x thuộc (a; b).
D. Hàm số \(y = f\left( x \right)\) đồng biến trên (a; b) khi và chỉ khi \(f'\left( x \right) > 0\) với mọi x thuộc (a; b).
Bài tập cuối chương I
QL
Cho hàm số y fleft( x right) có đạo hàm trên khoảng (a; b). Phát biểu nào dưới đây là đúng?A. Nếu fleft( x right) ge 0 với mọi x thuộc (a; b) thì hàm số y fleft( x right) đồng biến trên (a; b).B. Nếu fleft( x right) 0 với mọi x thuộc (a; b) thì hàm số y fleft( x right) đồng biến trên (a; b).C. Hàm số y fleft( x right) đồng biến trên (a; b) khi và chỉ khi fleft( x right) ge 0 với mọi x thuộc (a; b).D. Hàm số y fleft( x right) đồng biến trên (a; b) khi và chỉ khi fleft( x right) 0 với mọi x...
Đọc tiếp
Hướng dẫn giải
Thảo luận (1)
QL
Hàm số nào sau đây nghịch biến trên \(\mathbb{R}\)?
A. \(y = - {x^3} + 3{x^2} - 9x\);
B. \(y = - {x^3} + x + 1\);
C. \(y = \frac{{x - 1}}{{x - 2}}\);
D. \(y = 2{x^2} + 3x + 2\).
Hướng dẫn giải
Thảo luận (1)
Hàm số \(y = - {x^3} + 3{x^2} - 9x\) có:
\(y' = - 3{x^2} + 6x - 9 = - 3\left( {{x^2} - 2x + 1} \right) - 6 = - 3{\left( {x - 1} \right)^2} - 6 < 0\;\forall x \in \mathbb{R}\)
Do đó, hàm số \(y = - {x^3} + 3{x^2} - 9x\) nghịch biến trên \(\mathbb{R}\).
Chọn A.
Trả lời bởi Hà Quang Minh
QL
Hàm số nào dưới đây không có cực trị?
A. \(y = \left| x \right|\).
B. \(y = {x^4}\).
C. \(y = - {x^3} + x\).
D. \(y = \frac{{2x - 1}}{{x + 1}}\).
Hướng dẫn giải
Thảo luận (1)
Sử dụng kiến thức về định lí cực trị hàm số để tìm hàm không có cực trị: Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực tiểu của hàm số f(x).
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực đại của hàm số f(x).
Trả lời bởi Hà Quang Minh
QL
Giá trị cực tiểu của hàm số \(y = {x^2}\ln x\) là
A. \(\frac{1}{e}\).
B. \( - \frac{1}{e}\).
C. \( - \frac{1}{{2e}}\).
D. \(\frac{1}{{2e}}\).
Hướng dẫn giải
Thảo luận (1)
Tập xác định: \(D = \left( {0; + \infty } \right)\)
Ta có: \(y' = 2x\ln x + \frac{{{x^2}}}{x} = 2x\ln x + x = x\left( {2\ln x + 1} \right)\)
\(y' = 0 \Leftrightarrow x = \frac{1}{{\sqrt e }}\) (do \(x \in \left( {0; + \infty } \right)\))
Bảng biến thiên:
Trả lời bởi Hà Quang Minh
QL
Giá trị lớn nhất của hàm số \(y = {\left( {x - 2} \right)^2}.{e^x}\) trên đoạn [1; 3] là:
A. 0.
B. \({e^3}\).
C. \({e^4}\).
D. e.
Hướng dẫn giải
Thảo luận (1)
Ta có: \(y' = 2\left( {x - 2} \right){e^x} + {e^x}{\left( {x - 2} \right)^2},y' = 0 \Leftrightarrow 2\left( {x - 2} \right){e^x} + {e^x}{\left( {x - 2} \right)^2} = 0\)
\( \Leftrightarrow {e^x}\left( {2 + x - 2} \right)\left( {x - 2} \right) = 0 \Leftrightarrow x.{e^x}\left( {x - 2} \right) \Leftrightarrow x = 0\) hoặc \(x = 2\)
\(y\left( 0 \right) = 4;y\left( 1 \right) = e;y\left( 3 \right) = {e^3},y\left( 2 \right) = 0\)
Do đó, giá trị lớn nhất của hàm số \(y = {\left( {x - 2} \right)^2}.{e^x}\) trên đoạn [1; 3] là \({e^3}\).
Chọn B.
Trả lời bởi Hà Quang Minh
QL
Cho hàm số y fleft( x right) thỏa mãn: mathop {lim }limits_{x to {2^ + }} fleft( x right) 1;mathop {lim }limits_{x to {2^ - }} fleft( x right) 1;mathop {lim }limits_{x to - infty } fleft( x right) 2 và mathop {lim }limits_{x to + infty } fleft( x right) 2. Khẳng định nào sau đây là đúng?A. Đường thẳng x 2 là tiệm cận đứng của đồ thị hàm số.B. Đường thẳng y 2 là tiệm cận ngang của đồ thị hàm số.C. Đường thẳng y 1 là tiệm cận ngang của đồ thị hàm số.D. Đường thẳng x 2 là tiệm cận ngang...
Đọc tiếp
Cho hàm số \(y = f\left( x \right)\) thỏa mãn: \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 1;\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = 1;\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2\) và \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\). Khẳng định nào sau đây là đúng?
A. Đường thẳng \(x = 2\) là tiệm cận đứng của đồ thị hàm số.
B. Đường thẳng \(y = 2\) là tiệm cận ngang của đồ thị hàm số.
C. Đường thẳng \(y = 1\) là tiệm cận ngang của đồ thị hàm số.
D. Đường thẳng \(x = 2\) là tiệm cận ngang của đồ thị hàm số.
Hướng dẫn giải
Thảo luận (1)
Vì \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2\), \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\) nên đường thẳng \(y = 2\) là tiệm cận ngang của đồ thị hàm số, vì \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 1;\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = 1\) nên đồ thị hàm số \(y = f\left( x \right)\) không có tiệm cận đứng.
Chọn B.
Trả lời bởi Hà Quang Minh
QL
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 2x - 2}}{{x + 2}}\) là
A. \(y = - 2\).
B. \(y = 1\).
C. \(y = x + 2\).
D. \(y = x\).
Hướng dẫn giải
Thảo luận (1)
Ta có: \(y = \frac{{{x^2} + 2x - 2}}{{x + 2}} = x - \frac{2}{{x + 2}}\)
Lại có: \(\mathop {\lim }\limits_{x \to + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {x - \frac{2}{{x + 2}} - x} \right] = \mathop {\lim }\limits_{x \to + \infty } - \frac{2}{{x + 2}} = 0\)
\(\mathop {\lim }\limits_{x \to - \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {x - \frac{2}{{x + 2}} - x} \right] = \mathop {\lim }\limits_{x \to - \infty } - \frac{2}{{x + 2}} = 0\)
Do đó, đường thẳng \(y = x\) là tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 2x - 2}}{{x + 2}}\).
Chọn D.
Trả lời bởi Hà Quang Minh
QL
Cho hàm số y fleft( x right) xác định trên mathbb{R}backslash left{ {1;3} right}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:Khẳng định nào sau đây là sai?A. Đường thẳng y 1 là tiệm cận ngang của đồ thị hàm số đã cho.B. Đường thẳng y - 1 là tiệm cận ngang của đồ thị hàm số đã cho.C. Đường thẳng x 3 là tiệm cận đứng của đồ thị hàm số đã cho.D. Đường thẳng x 1 là tiệm cận đứng của đồ thị hàm số đã cho.
Đọc tiếp
Cho hàm số \(y = f\left( x \right)\) xác định trên \[\mathbb{R}\backslash \left\{ {1;3} \right\}\], liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

Khẳng định nào sau đây là sai?
A. Đường thẳng \(y = 1\) là tiệm cận ngang của đồ thị hàm số đã cho.
B. Đường thẳng \(y = - 1\) là tiệm cận ngang của đồ thị hàm số đã cho.
C. Đường thẳng \(x = 3\) là tiệm cận đứng của đồ thị hàm số đã cho.
D. Đường thẳng \(x = 1\) là tiệm cận đứng của đồ thị hàm số đã cho.
Hướng dẫn giải
Thảo luận (1)
Vì \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = - 1;\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = 7\) nên đường thẳng \(x = 1\) không phải là tiệm cận đứng của đồ thị hàm số đã cho.
Chọn D.
Trả lời bởi Hà Quang Minh
QL
Đồ thị trong Hình 1.37 là đồ thị của hàm số:
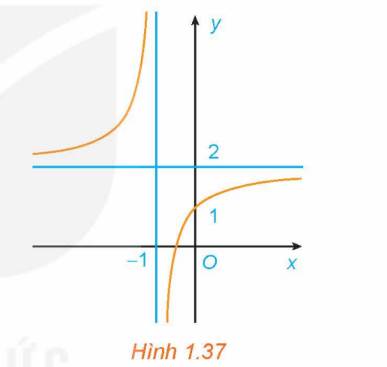
A. \(y = \frac{{x + 2}}{{x + 1}}\).
B. \(y = \frac{{2x + 1}}{{x + 1}}\).
C. \(y = \frac{{x - 1}}{{x + 1}}\).
D. \(y = \frac{{x + 3}}{{1 - x}}\).
Hướng dẫn giải
Thảo luận (1)
Đồ thị hàm số trong hình 1.37 có tiệm cận ngang là \(y = 2\).
Xét hàm số: \(y = \frac{{2x + 1}}{{x + 1}}\) có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 + \frac{1}{x}}}{{1 + \frac{1}{x}}} = 2\) nên đồ thị hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) có tiệm cận ngang là \(y = 2\).
Đường thẳng \(y = 2\) không là tiệm cận ngang của các đồ thị hàm số \(y = \frac{{x - 1}}{{x + 1}}\); \(y = \frac{{x + 3}}{{1 - x}}\); \(y = \frac{{x + 2}}{{x + 1}}\).
Chọn B.
Trả lời bởi Hà Quang Minh
QL
Đồ thị trong Hình 1.38 là đồ thị của hàm số:
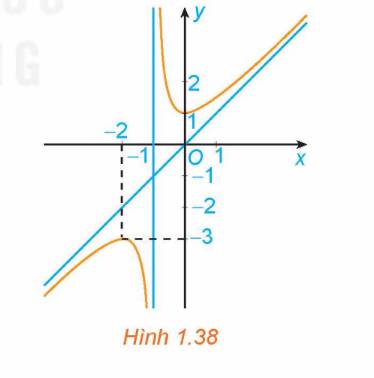
A. \(y = x - \frac{1}{{x + 1}}\).
B. \(y = \frac{{2x + 1}}{{x + 1}}\).
C. \(y = \frac{{{x^2} - x + 1}}{{x + 1}}\).
D. \(y = \frac{{{x^2} + x + 1}}{{x + 1}}\).
Hướng dẫn giải
Thảo luận (1)
Đồ thị hàm số trong hình 1.38 có dạng: \(y = \frac{{a{x^2} + bx + c}}{{px + q}}\left( {a \ne 0,p \ne 0} \right)\) và đa thức tử không chia hết cho đa thức mẫu. Do đó, loại đáp án B.
Đồ thị hàm số trong hình 1.38 đi qua điểm \[\left( { - 2; - 3} \right)\]. Do đó, loại đáp án C.
Đồ thị hàm số trong hình 1.38 đi qua điểm (0; 1). Do đó, loại đáp án A.
Hàm số \(y = \frac{{{x^2} + x + 1}}{{x + 1}} = x + \frac{1}{{x + 1}}\) có:
+ \(\mathop {\lim }\limits_{x \to - {1^ + }} \frac{{{x^2} + x + 1}}{{x + 1}} = + \infty ;\mathop {\lim }\limits_{x \to - {1^ - }} \frac{{{x^2} + x + 1}}{{x + 1}} = - \infty \) nên đường thẳng \(x = - 1\) là tiệm cận đứng của đồ thị hàm số.
+ \(\mathop {\lim }\limits_{x \to + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {x + \frac{1}{{x + 1}} - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x + 1}} = 0\), \(\mathop {\lim }\limits_{x \to - \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {x + \frac{1}{{x + 1}} - x} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x + 1}} = 0\) nên đường thẳng \(y = x\) là tiệm cận xiên của đồ thị hàm số.
Chọn D.
Trả lời bởi Hà Quang Minh
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng (a; b). Nếu \(f'\left( x \right) > 0\) với mọi x thuộc (a; b) thì hàm số \(y = f\left( x \right)\) đồng biến trên (a; b).
Chọn B.
Trả lời bởi Hà Quang Minh