Kết luận nào sau đây đúng khi nói về đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)?
A. Với a > 0, đồ thị nằm phía trên trục hoành và O là điểm cao nhất của đồ thị.
B. Với a < 0, đồ thị nằm phía dưới trục hoành và O là điểm thấp nhất của đồ thị.
C. Với a > 0, đồ thị nằm phía dưới trục hoành và O là điểm thấp nhất của đồ thị.
D. Với a < 0, đồ thị nằm phía dưới trục hoành và O là điểm cao nhất của đồ thị.
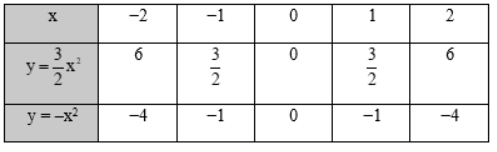
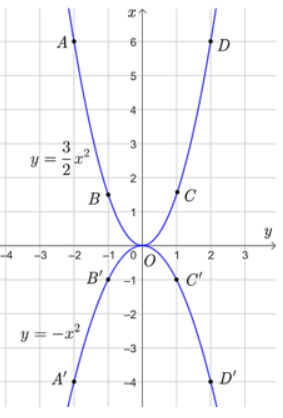
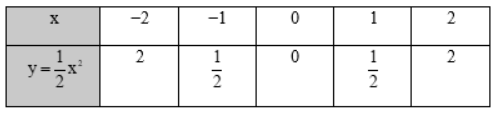
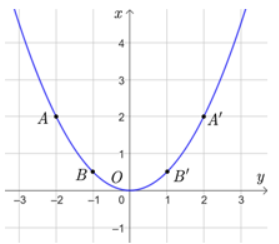
Chọn đáp án D.
Trả lời bởi datcoder