Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm D, G sao AD = CG < AC. Từ điểm D kẻ DE vuông góc với AC (E thuộc AB). Chứng minh tứ giác CDEG là hình chữ nhật.
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ < AB. Chứng minh tứ giác MNPQ là hình vuông.
Ta có: AM = BN = CP = DQ (gt)
AB = BC = CD = DA (ABCD là hình vuông)
\(\Rightarrow\) BM = CN = DP = AQ
\(\Rightarrow \Delta AMQ = \Delta BNM = \Delta CPN = \Delta DQP\)(hai cạnh góc vuông)
Suy ra QM = MN = NP = PQ
Suy ra MNPQ là hình thoi
Do: \(\Delta AMQ = \Delta BNM \Rightarrow {\widehat M_1} = \widehat {BNM}\) (2 góc tương ứng)
Mà: \(\widehat {BNM} + {\widehat M_3} = {90^0}\)(do \(\Delta BNM\)vuông tại B)
\( \Rightarrow {\widehat M_1} + {\widehat M_3} = {90^0} \Rightarrow {\widehat M_2} = {180^0} - {\widehat M_1} - {\widehat M_3} = {180^0} - {90^0} = {90^0}\)
Vậy hình thoi MNPQ có một góc bằng 90o nên MNPQ là hình vuông
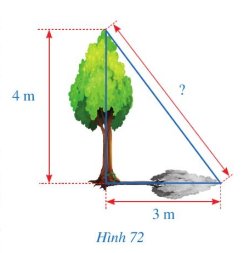
Trả lời bởi Hà Quang MinhHình 72 mô tả một cây cao 4m. Biết rằng khi trời nắng, cây đổ bóng trên mặt đất, điểm xa nhất của bóng cây cách gốc cây một khoảng là 3 m. Tính khoảng cách từ điểm xa nhất của bóng cây đến đỉnh của cây.
Khoảng cách từ điểm xa nhất của bóng cây đến đỉnh cây bằng \(\sqrt{3^2+4^2}=5\left(m\right)\) (áp dụng định lý Py-ta-go).
Trả lời bởi Hà Quang MinhCho hình chữ nhật ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh tứ giác MNPQ là hình thoi.
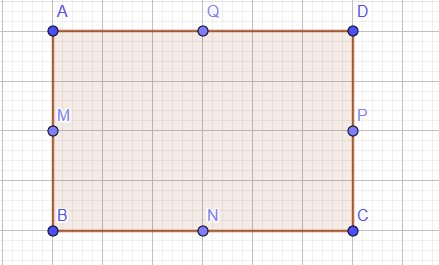
Áp dụng định lý Pytago: `QM = sqrt(AQ^2 + AM^2) = sqrt(((AB)/2)^2 + ((AD)/2)^2).`
`MN = sqrt(BM^2 + NB^2) = sqrt(((AB)/2)^2 + ((BC)/2)^2) = sqrt(((AB)/2)^2 + ((AD)/2)^2)`.
Chứng minh tương tự cho `NP, QP` ta thấy `QM = MN = NP = QP`.
Vậy tứ giác MNPQ là hình thoi.
Trả lời bởi Vui lòng để tên hiển thịMàn hình một chiếc ti vi có dạng hình chữ nhật với kích thước màn hình ti vi được tính bằng độ dài đường chéo của màn hình (đơn vị: inch, trong đó 1 inch = 2, 54m). Người ta đưa ra công thức tính khoảng cách an toàn khi xem ti vi để giúp khách hàng lựa chọn được chiếc ti vi phù hợp với căn phòng của mình như sau:
Khoảng cách tối thiểu = 5, 08 . d (cm)
Khoảng cách tối đa = 7, 62 . d (cm)
Trong đó, d là kích thước màn hình ti vi tính theo inch.
Với một chiếc ti vi có chiều dài màn hình 74, 7 cm, chiều rộng màn hình 32 cm;
a) Kích thước màn hình của ti vi đó là bao nhiêu inch (làm tròn kết quả đến hàng đơn vị)?
b) Khoảng cách tối thiểu và khoảng cách tối đa để xem chiếc ti vi đó là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
a, Vì ti vi là hình chữ nhật nên đường chính là đường chéo của hình chữ nhật đó
Khi đó \({d^2} = \sqrt {74,{7^2} + {{32}^2}} \approx 81(cm)\)
Đổi 81cm = \( \frac {81} {2,54} \approx \) 32inch
b, Khoảng cách tối thiểu là:
\(5,08.32 = 162,56(cm) \approx 1,6m \)
Khoảng cách tối đa là:
\(7,62.32 = 243,84(cm) \approx 2,4m\)
Trả lời bởi Hà Quang MinhCho hình chữ nhật MNPQ. Đoạn thẳng MP bằng đoạn thẳng nào sau đây:
A. NQ
B. MN
C. NP
D. QM
Cho hình thang cân ABCD có AB // CD, \(\widehat A = {80^o}\). Khi đó, \(\widehat C\) bằng:
A. 80o
B. 90o
C. 100o
D. 110o
Vì ABCD là hình thang cân nên \(\widehat A = \widehat B = {80^o}\)
Khi đó: \(\widehat C = \widehat D = \frac{{{{360}^o} - \widehat B - \widehat A}}{2} = \frac{{{{360}^o} - {{80}^o} - {{80}^o}}}{2} = {100^o}\left( {\widehat A + \widehat B + \widehat C + \widehat D = {{360}^o}} \right)\)
Chọn đáp án C
Trả lời bởi Hà Quang MinhCho tứ giác ABCD có \(\widehat A = {60^o},\widehat B = {70^o},\widehat C = {80^o}\). Khi đó, \(\widehat D\) bằng:
A. 130o
B. 140o
C. 150o
D. 160o
ABCD là tứ giác nên:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\\ \Rightarrow \widehat D = {360^o} - \widehat A - \widehat B - \widehat C = {360^o} - {60^o} - {70^o} - {80^o} = {150^o}\end{array}\)
Chọn đáp án C
Trả lời bởi Hà Quang MinhCho hình bình hành MNPQ có các góc khác 90o, MP cắt NQ tại I. Khi đó:
A. IM = IN
B. IM = IP
C. IM = IQ
D. IM = MP
Hình bình hành MNPQ có các góc khác 90o, MP cắt NQ tại I. Khi đó: IM = IP; IN = IQ
Chọn đáp án B
Trả lời bởi Hà Quang MinhCho tứ giác ABCD có \(\widehat {DAB} = \widehat {BC{\rm{D}}};\widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\). Chứng minh ABCD là hình bình hành.
Xét \(\Delta ABD\)có: \(\widehat {BAD} + \widehat {ABD} + \widehat {BDA} = {180^0}\)
Xét \(\Delta BCD\)có: \(\widehat {BCD} + \widehat {BDC} + \widehat {DBC} = {180^0}\)
\(\begin{array}{l} \Rightarrow \widehat {BAD} + \widehat {ABD} + \widehat {BDA} = \widehat {BCD} + \widehat {BDC} + \widehat {DBC}\\ \Rightarrow \widehat {DAB} = \widehat {DBC}(do\,\widehat {BAD} = \widehat {BCD};\widehat {ABD} = \widehat {BDC})\end{array}\)
Xét \(\Delta ABD\) và \(\Delta CDB\) có:
\(\begin{array}{l}\left. \begin{array}{l}\widehat {ABD} = \widehat {CDB}\\BDchung\\\widehat {DBA} = \widehat {DBC}\end{array} \right\} \Rightarrow \Delta ABD = \Delta CDB(g.c.g)\\ \Rightarrow AB = DC\\AD = CB\end{array}\)
Suy ra tứ giác ABCD là hình bình hành vì có cặp cạnh đối bằng nhau
Trả lời bởi Hà Quang Minh
Vì \(\Delta ABC\) vuông cân tại C.
\( \Rightarrow \widehat {C{\rm{AB}}} = {45^0} \Rightarrow \widehat {DA{\rm{E}}} = {45^0}\)
\(\Rightarrow \widehat {DE{\rm{A}}} = {45^0} \Rightarrow \Delta ADE\) là tam giác vuông cân tại D
Suy ra AD = DE (1)
Mà: AD = CG (2)
Từ (1), (2) suy ra: DE = CG.
Mặt khác DE//CG (vì cùng vuông góc với AC)
Suy ra tứ giác CDEG là hình bình hành
Mặt khác: \(\widehat {DCG} = {90^0}\)
Suy ra hình bình hành CDEG là hình chữ nhật
Trả lời bởi Hà Quang Minh