Trung đoạn của hình chóp tam giác đều trong Hình 10.34 là:
A. SB
B. SH
C. SI
D. HI
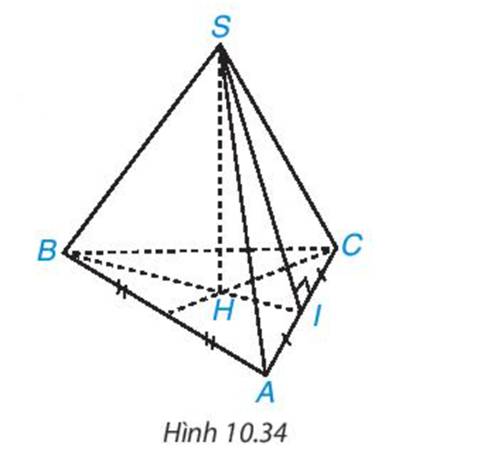
Trung đoạn của hình chóp tam giác đều trong Hình 10.34 là:
A. SB
B. SH
C. SI
D. HI

Đáy của hình chóp tứ giác đều là:
A. Hình vuông
B. Hình bình hành
C. Hình thoi
D. Hình chữ nhật
Phương án A là phương án đúng
Trả lời bởi Hà Quang MinhDiện tích xung quanh của hình chóp tam giác đều bằng:
A. Tích của nửa chu vi đáy và chiều cao của hình chóp
B. Tích của nửa chu vi và trung đoạn
C. Tích của chu vi đáy và trung đoạn
D. Tổng của chu vi đáy và trung đoạn
Diện tích xung quanh của hình chóp tam giác đều bằng tích của nửa chu vi và trung đoạn => phương án B
Trả lời bởi Hà Quang MinhMột hình chóp tam giác đều có chiều cao h, thể tích V. Diện tích đáy S là:
A. \(S = \frac{h}{V}\)
B. \(S = \frac{V}{h}\)
C. \(S = \frac{{3V}}{h}\)
D. \(S = \frac{{3h}}{V}\)
Ta có: \(V = \frac{1}{3}.S.h \Rightarrow S = \frac{{3V}}{h} \Rightarrow \) Phương án C
Trả lời bởi Hà Quang MinhGọi tên đỉnh, cạnh bên, cạnh đáy, đường cao và một trung đoạn của hình chóp tam giác đều, hình chóp tứ giác đều.
Hình chóp tam giác đều
- Đỉnh: S
- Cạnh bên: SD, SE, SF
- Cạnh đáy: DE, DF, EF
- Đường cao: SO
- Một trung đoạn: SH
Trả lời bởi Quoc Tran Anh LeTính diện tích xung quanh của hình chóp tam giác đều, hình chóp tứ giác đều trong Hình 10.36.
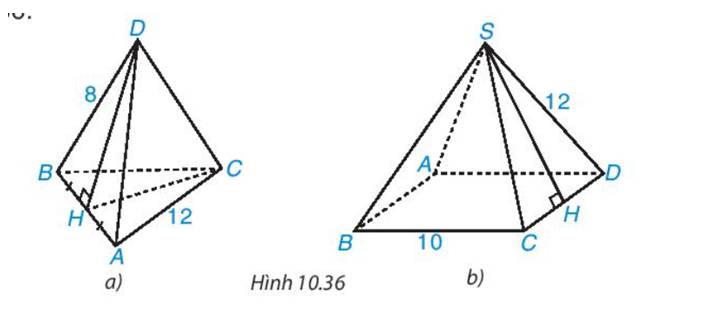
* Nửa chu vi của tam giác ABC là:
\(\left( {12 + 12 + 12} \right):2 = 18(m)\)
Xét tam giác HBD vuông tại H, có:
\(\begin{array}{l}H{{\rm{D}}^2} = B{{\rm{D}}^2} - B{H^2} = {8^2} - {6^2}\\ \Rightarrow H{\rm{D}} = 2\sqrt 7 \end{array}\)
Diện tích xung quanh của hình chóp tam giác đều là:
\({S_{xq}} = p.d = 18.2\sqrt 7 = 36\sqrt 7 \left( {{m^2}} \right)\)
* Nủa chu vi của tứ giác ABCD là:
\(\left( {10.4} \right):2 = 20\)
Xét tam giác SHD vuông tại H, ta có:
\(\begin{array}{l}S{H^2} = S{{\rm{D}}^2} - H{{\rm{D}}^2} = {12^2} - {6^2} = 119\\ \Rightarrow SH = \sqrt {119} \end{array}\)
Diện tích xung quanh của hình chóp tứ giác đều là:
\({S_{xq}} = p.d = 20.\sqrt {119} = 20\sqrt {119} \left( {{m^2}} \right)\)
Trả lời bởi Hà Quang MinhTính thể tích của hình chóp tứ giác đều, biết chiều cao bằng 9 cm và chu vi đáy bằng 12 cm.
Có chu vi đáy bằng 12 cm => Cạnh của đáy là: 12:4=3 (cm) (vì đáy của hình chóp tứ giác đều là hình vuông)
- Diện tích đáy là: 3.3=9 (cm2)
- Thể tích hình chóp là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.9.9 = 27\left( {c{m^3}} \right)\)
Trả lời bởi Hà Quang MinhTừ một khúc gỗ hình lập phương cạnh 30 cm, người ta cắt đi một phần gỗ để được phần còn lại là một hình chóp tứ giác đều có đáy là hình vuông cạnh 30 cm và chiều cao của hình chóp cũng bằng 30 cm. Tính thể tích của phần gỗ bọ cắt đi.
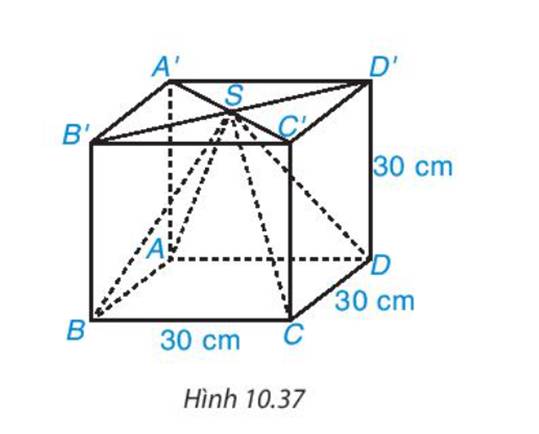
Diện tích mặt đáy của hình chóp tứ giác đều ABCD là: 30.30=900 (cm2)
- Thể tích hình chóp là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.900.30 = 9000(c{m^3})\)
- Thể tích hình lập phương là V=30.30.30=27000 (cm3)
Vậy thể tích phần gỗ bị cắt đi là V = 27000 − 9000=18000 (cm3)
Trả lời bởi Hà Quang MinhMột khối gỗ gồm đế là hình lập phương cạnh 9 cm và một hình chóp tứ giác đều. Tính thể tích khối gỗ.
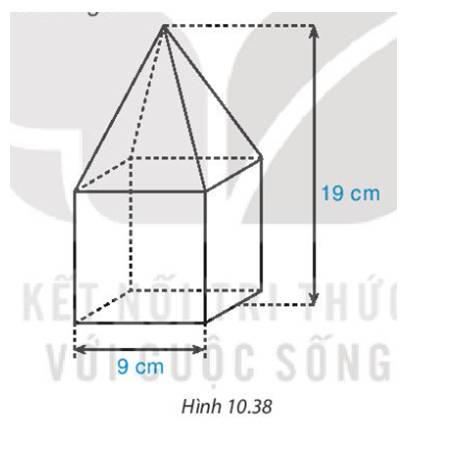
Có chiều cao của cả khối gỗ là 9 cm, chiều cao cụa hình lập phương là 9 cm
=> Chiều cao của hình chóp tứ giác đều là: 19−9=10 (cm)
- Diện tích mặt đáy của hình chóp tứ giác đều là: 9.9=81 (cm2)
- Thể tích hình chóp là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.81.10 = 270\left( {c{m^3}} \right)\)
- Thể tích hình lập phương là: V=9.9.9=729 \(\left( {c{m^3}} \right)\)
Vậy thể tích của khối gỗ là: 270+729= 999 (cm3)
Trả lời bởi Hà Quang MinhBạn Trang cắt miếng bìa hình tam giác đều cạnh dài 20 cm và gấp lại theo các dòng kẻ (nét đứt) để được hình chóp tam giác đều. Tính diện tích xung quanh của hình chóp tam giác đều tạo thành. Cho biết \(\sqrt {75} \approx 8,66\)
Các mặt bên của hình chóp là tam giác giác đều cạnh là 10 cm => Đường cao trong một mặt tam giác là: \(\sqrt {{{10}^2} - {5^2}} = \sqrt {75} \approx 8,66\) cm
Các nét đứt tạo thành mặt đáy của hình chóp tam giác đều có cạnh là 10 cm => Nửa chu vi mặt đáy là:
\(\frac{1}{2}.\left( {10 + 10 + 10} \right) = 15\left( m \right)\)
Vậy diện tích xung quanh là: \(S_{xq}=p.d=15.8,66=129,9 (c{m^2})\)
Trả lời bởi Hà Quang Minh
Trung đoạn là SI => C là phương án đúng
Trả lời bởi Hà Quang Minh