Hãy gọi tên đỉnh, cạnh bên, mặt bên, mặt đáy, đường cao, đường trung bình của hình chóp tam giác đều S. ABC tronh hình 10.2.
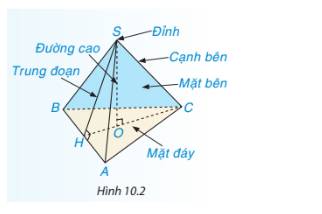
Hãy gọi tên đỉnh, cạnh bên, mặt bên, mặt đáy, đường cao, đường trung bình của hình chóp tam giác đều S. ABC tronh hình 10.2.

Quan sát hình chóp tam giác đều và hình khai triển của nó. Hãy tính tổng diện tích các mặt bên của hình chóp.
Nhận thấy các mặt bên của hình chóp được tạo bởi 3 hình tam giác
Diện tích của một tam giác là: \(\frac{1}{2}\)⋅6⋅5=15(cm2)
=> Tổng diện tích các mặt bên là: 15.3=45(cm2)
Trả lời bởi Hà Quang MinhHãy tính tích của nửa chu vi mặt đáy với trung đoạn của hình chóp tam giác đều. So sánh kết quả vừa tính với tổng diện tích các mặt bên của hình chóp.
Có nửa chu vi đáy là: \(\frac{1}{2}.\)(5+5+5) = \(\frac{{15}}{2}\)(cm)
Có trung đoạn là: 6cm
=> Tích của nửa chu vi mặt đáy với trung đoạn của hình chóp tam giác đều là: \(\frac{{15}}{2}.6 = 45\)
=> Kết quả bằng với tổng diện tích các mặt bên của hình chóp
Trả lời bởi Hà Quang MinhTính diện tích xung quanh của hình chóp tam giác đều S.MNP trong Hình 10.8, biết IP = 3 cm và cạnh bên SP = 5 cm
Xét tam giác SIP vuông tại I, có
\(\begin{array}{l}S{I^2} = S{P^2} - I{P^2}\\S{I^2} = {5^2} - {3^2}\\ \Rightarrow SI = 4cm\end{array}\)
- Vì tam giác SMP cân tại S => đường cao SI đồng thời là đường trung tuyến của tam giác SMP => IM=IP=3cm => MP = 6 cm
Xét tam giác đều MNP có \(p = \frac{1}{2}\left( {6 + 6 + 6} \right) = 9(cm)\)
Diện tích xung quanh của hình chóp tam giác đều S. MNP:
\({S_{xp}} = 9.4 = 36\left( {c{m^2}} \right)\)
Trả lời bởi Hà Quang MinhĐỉnh Fansipan (Lào Cai) cao 3 143m, là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi. người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều cạnh đáy 60 cm, chiều cao 90 m. Hỏi tổng diện tích các mặt bên của hình chóp là bao nhiêu.
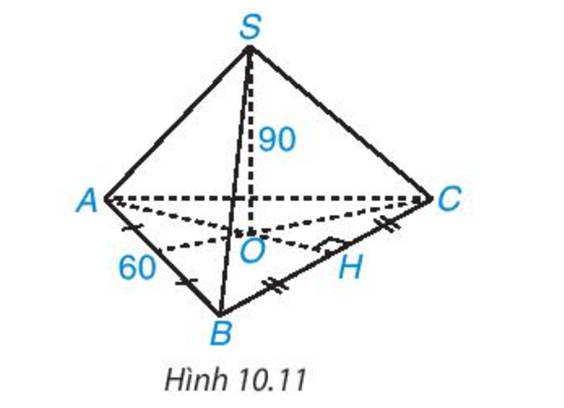
Nửa chu vi của hình tam giác đều ABC là:
\(p = \frac{1}{2}\left( {60 + 60 + 60} \right) = 90(cm)\)
Diện tích xung quanh của hình chóp tam giác đều S. ABC là:
\({S_{xq}} = 90.90 = 8100(c{m^2})\)
Vậy diện tích các mặt bên của hình chóp tam giác đều là 8100 cm2
Trả lời bởi Hà Quang MinhGọi tên đỉnh, cạnh bên, mặt bên, mặt đáy, đường cao và một trung đoạn của hình chóp tam giác giác đều trong Hình 10.12.
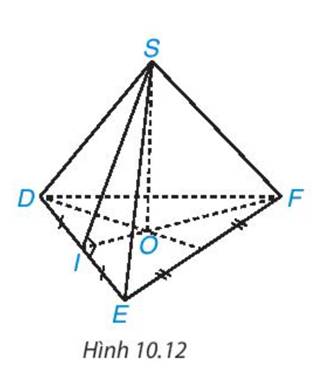
- Đỉnh: S
- Cạnh bên: SD, SE, SF
- Mặt bên: SDE, SEF, SDF
- Mặt đáy: DEF
- Đường cao: SO
- Một trung đoạn: SI
Trả lời bởi Hà Quang MinhVẽ và cắt một tam giác đều có cạnh 10 cm (H10.13) rồi gấp theo đường màu cam để được hình chóp tam giác đều (H.10.14)
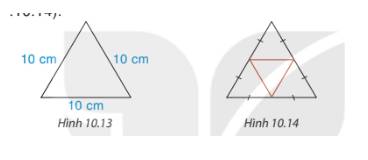
Vẽ và cắt theo yêu cầu của đề bài.
Trả lời bởi Hà Quang MinhCho hình chóp tam giác đều S.MNP như H.10.15
a) Tính diện tích tam giác MNP
b) Tính thể tích hình chóp S.MNP, biết \(\sqrt {27} = 5,19\)
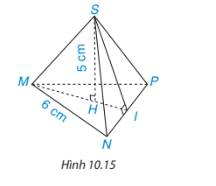
Vì tam giác MNP đều
=> MN=NP=MP=6cm
=> IN=IP=3cm
Xét tam giác MIN vuông tại I, có:
\(\begin{array}{l}M{I^2} = M{N^2} - I{N^2} = {6^2} - {3^2}\\ \Rightarrow MI = 5,2\\ \Rightarrow {S_{MNP}} = \frac{1}{2}.MI.NP = \frac{1}{2}.5,2.6 = 15,6(c{m^2})\\ \Rightarrow V = \frac{1}{3}.S.h = \frac{1}{2}.15,6.5 = 26(c{m^3})\end{array}\)
Trả lời bởi Hà Quang MinhNhà bạn Thu có một đèn trang trí có dạng hình chóp tam giác đều. Các cạnh của hình chóp đều bằng nhau và bằng 20 cm. Bạn Thu dự định sẽ dán các mặt bên của đèn bằng những tấm giấy màu. Tính diện tích giấy bạn Thu sử dụng (coi như mép dán không đáng kể). Cho biết \(\sqrt {300} = 17,32\)
- Chiều cao của đèn là: \(h = \sqrt {{{20}^2} - {{10}^2}} = 10\sqrt 3 = 17,32\)
- Có diện tích của một mặt bên là: \(\frac{1}{2}.17,32.20 = 173,2(c{m^2})\)
=> Diện tích các mặt bên là: 173,2.3 = 519,6 (cm2)
Trả lời bởi Hà Quang Minh
Hình chóp tam giác đều S. ABC có:
- Đỉnh: S
- Cạnh bên: SA, SB, SC.
- Mặt đáy: tam giác ABC.
- Đường cao: SO.
- Trung đoạn: SH
Trả lời bởi Hà Quang Minh