Cho hai tam giác ABC và A’B’C’ sao cho ba đường thẳng AA’, BB’, CC’ cùng đi qua điểm O và \(\dfrac{OA'}{OA}=\dfrac{OB'}{OB}=\dfrac{OC'}{OC}=3\) (Hình 91). Tam giác A’B’C’ nhận được từ tam giác ABC bằng cách nào?
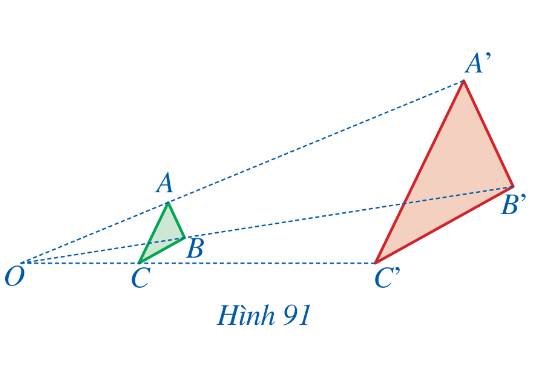
Cho hai tam giác ABC và A’B’C’ sao cho ba đường thẳng AA’, BB’, CC’ cùng đi qua điểm O và \(\dfrac{OA'}{OA}=\dfrac{OB'}{OB}=\dfrac{OC'}{OC}=3\) (Hình 91). Tam giác A’B’C’ nhận được từ tam giác ABC bằng cách nào?

Cho hai tứ giác ABCD và A’B’C’D’ sao cho bốn đường thẳng AA’, BB’, CC’, DD’ cùng đi qua điểm O và \(\dfrac{OA'}{OA}=\dfrac{OB'}{OB}=\dfrac{OC'}{OC}=\dfrac{OD'}{OD}=\dfrac{1}{2}\) (Hình 92). Tứ giác A’B’C’D’ có thể nhận được từ tứ giác ABCD bằng cách nào?
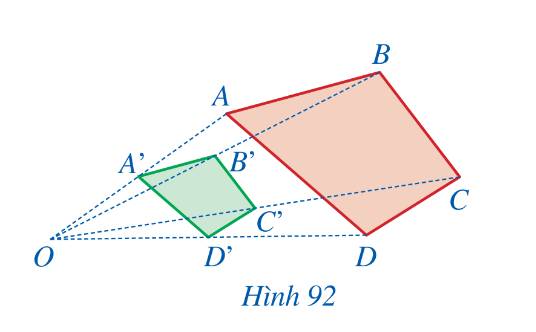
Từ điểm O, ‘‘thu nhỏ’’ hai lần tứ giác ABCD, ta sẽ nhận được tứ giác A’B’C’D’.
Trả lời bởi Hà Quang MinhThực hiện các hoạt động sau.
a) Cắt ra từ tờ giấy kẻ ô vuông:
– Hình chữ nhật ABCD có AB = 3 cm, AD = 2 cm; hình chữ nhật A’B’C’D’ có A’B’ = 3 cm, A’D’ = 2 cm;
– Hình vuông MNPQ có MN = 4 cm; hình vuông M’N’P’Q’ có M’N’ = 4 cm.
b) – Đặt hai mảnh giấy hình chữ nhật ABCD và A’B’C’D’ "chồng khít" lên nhau.
– Đặt hai mảnh giấy hình vuông MNPQ và M’N’P’Q’ "chồng khít" lên nhau.
Thực hiện theo hướng dẫn của GV và SGK.
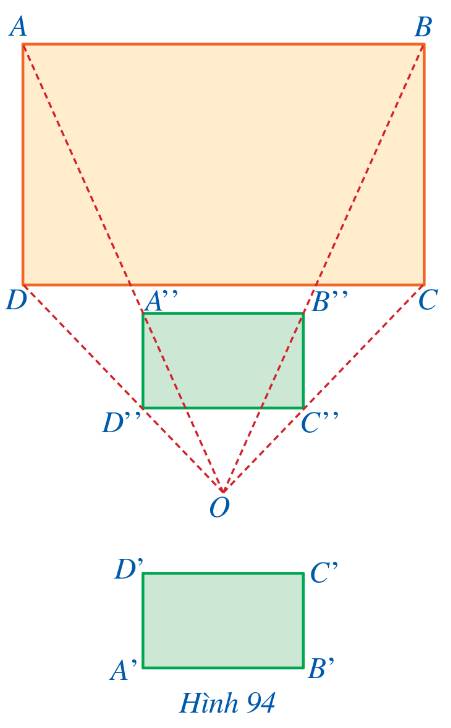
Trả lời bởi Hà Quang MinhTrong Hình 94, hình chữ nhật ABCD có AB = 9 cm, AD = 6 cm; hình chữ nhật A’B’C’D’ có A’B’ = 3 cm, A’D’ = 2 cm; hình chữ nhật A’’B’’C’’D’’ có A’’B’’ = 3 cm, A’’D’’ = 2 cm. Quan sát Hình 94 và cho biết:
a) Hai hình chữ nhật A’’B’’C’’D’’, ABCD có đồng dạng phối cảnh hay không.
b) Hai hình chữ nhật A’B’C’D’, A’’B’’C’’D’’ có bằng nhau hay không.
a: Xét ΔODC có D''C''//DC
nên \(\dfrac{D''C''}{DC}=\dfrac{OD''}{OD}=\dfrac{OC''}{OC}=\dfrac{3}{9}=\dfrac{1}{3}\)(1)
Xét ΔOAB có A''B"//AB
nên \(\dfrac{A"B"}{AB}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}=\dfrac{3}{9}=\dfrac{1}{3}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{OD"}{OD}=\dfrac{OC"}{OC}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}\)
mà A"A, B"B, C"C, D"D đều đi qua điểm O
nên hai hình hộp chữ nhật A"B"C"D" và ABCD đồng dạng phối cảnh với nhau
b: ta có: A'B'=C'D'=3cm
A"B"=C"D"=3cm
Do đó: A"B"=C"D"=A'B'=C'D'(3)
ta có: A'D'=B'C'=2cm
A"D"=B"C"=2cm
Do đó: A'D'=B'C'=A"D"=B"C"(4)
Từ (3),(4) suy ra hai hình hộp chữ nhật A"B"C"D" và A'B'C'D' bằng nhau
Trả lời bởi Nguyễn Lê Phước Thịnh
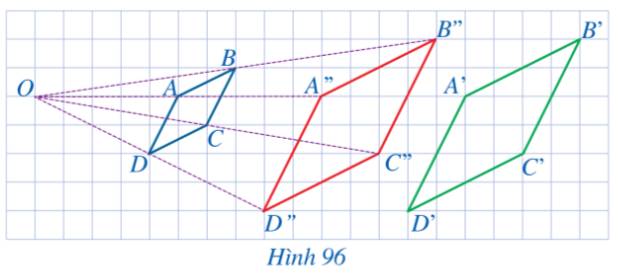
Trong Hình 96, các điểm A, B, C, D lần lượt là trung điểm của các đoạn thẳng OA'', OB'', OC'', OD''. Quan sát Hình 96 và cho biết:
a) Hai hình thoi A'B'C'D' và A''B''C''D'' có bằng nhau hay không?
b) Hai hình thoi A'B'C'D' và ABCD có đồng dạng hay không?
a) Hình thoi A'B'C'D' bằng hình thoi A''B''C''D''.
b) Ta thấy hình thoi A''B''C''D'' đồng dạng phối cảnh với hình thoi ABCD
Mà hình thoi A'B'C'D' bằng hình thoi A''B''C''D''
\( \Rightarrow \)Hình thoi A'B'C'D' đồng dạng với hình thoi ABCD.
Trả lời bởi Hà Quang MinhCho tam giác ABC có \(AB = 3,{\rm{ }}BC = 6,{\rm{ }}CA = 5\). Cho O, I là hai điểm phân biệt.
a) Giả sử tam giác A'B'C' là hình đồng dạng phối cảnh của tam giác ABC với điểm O là tâm đồng dạng phối cảnh, tỉ số \(\frac{{A'B'}}{{AB}} = 3\). Hãy tìm độ dài các cạnh của tam giác A'B'C'.
b) Giả sử tam giác A''B''C'' là hình đồng dạng phối cảnh của tam giác ABC với điểm I là tâm đồng dạng phối cảnh, tỉ số \(\frac{{A'B'}}{{AB}} = 3\). Hãy tìm độ dài các cạnh của tam giác A''B''C''.
c) Chứng minh \(\Delta A'B'C' = \Delta A''B''C''\)
Chú ý: Hai tam giác cùng là hình đồng dạng phối cảnh tỉ số k (tâm đồng dạng phối cảnh có thể khác nhau) của một tam giác luôn bằng nhau
a) Vì tam giác A'B'C' là hình đồng dạng phối cảnh của tam giác ABC nên \(\Delta A'B'C' \backsim \Delta ABC\).
\(\begin{array}{l} \Rightarrow \frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{C'A'}}{{CA}} = 3\\ \Rightarrow \frac{{A'B'}}{3} = \frac{{B'C'}}{6} = \frac{{C'A'}}{5} = 3\\ \Rightarrow A'B' = 9,\,\,B'C' = 18,\,\,C'A' = 15\end{array}\)
b) Vì tam giác A”B”C” là hình đồng dạng phối cảnh của tam giác ABC nên \(\Delta A''B''C'' \backsim \Delta ABC\).
\(\begin{array}{l} \Rightarrow \frac{{A''B''}}{{AB}} = \frac{{B''C''}}{{BC}} = \frac{{C''A''}}{{CA}} = 3\\ \Rightarrow \frac{{A''B''}}{3} = \frac{{B''C''}}{6} = \frac{{C''A''}}{5} = 3\\ \Rightarrow A''B'' = 9,\,\,B''C'' = 18,\,\,C''A'' = 15\end{array}\)
c) Ta có:
\(\begin{array}{l}A'B' = A''B'' = 9\\B'C' = B''C'' = 18\\C'A' = C''A'' = 15\end{array}\)
\( \Rightarrow \Delta A'B'C' = \Delta A''B''C''\)(c-c-c)
Trả lời bởi Hà Quang MinhCho hai hình chữ nhật ABCD và A'B'C'D' có \(\frac{{A'B'}}{{B'C'}} = \frac{{AB}}{{BC}}\). Trên các tia AB, AC, AD ta lần lượt lấy các điểm B'', C'', D'' sao cho \(\frac{{AB''}}{{AB}} = \frac{{AC''}}{{AC}} = \frac{{AD''}}{{AD}} = \frac{{B'C'}}{{BC}}\). Chứng minh:
a) Hình chữ nhật AB''C''D'' đồng dạng phối cảnh với hình chữ nhật ABCD;
b) AB'' = A'B', B''C'' = B'C'
c) Hai hình chữ nhật ABCD và A'B'C'D' là đồng dạng
a) Vì \(\frac{{AB''}}{{AB}} = \frac{{AC''}}{{AC}} = \frac{{AD''}}{{AD}}\) nên hình chữ nhật AB”C”D” đồng dạng phối cảnh với hình chữ nhật ABCD.
b) Ta có: \(\frac{{A'B'}}{{B'C'}} = \frac{{AB}}{{BC}} \Rightarrow \frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}}\)
Mà \(\frac{{AB''}}{{AB}} = \frac{{B'C'}}{{BC}} \Rightarrow A'B' = AB''\)
Ta có hình chữ nhật AB”C”D” đồng dạng phối cảnh với hình chữ nhật ABCD
\( \Rightarrow \frac{{B''C''}}{{BC}} = \frac{{AB''}}{{AB}}\)
Mà \(\frac{{AB''}}{{AB}} = \frac{{B'C'}}{{BC}} \Rightarrow \frac{{B''C''}}{{BC}} = \frac{{B'C'}}{{BC}} \Rightarrow B''C'' = B'C'\)
c) Ta có: \(\frac{{A'B'}}{{B'C'}} = \frac{{AB}}{{BC}} \Rightarrow \frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}}\)
Vậy hình chữ nhật ABCD đồng dạng với hình chữ nhật A’B’C’D’.
Trả lời bởi Hà Quang Minh
Từ điểm O, ‘‘phóng to’’ ba lần tam giác ABC, ta sẽ nhận được tam giác A’B’C’.
Trả lời bởi Hà Quang Minh