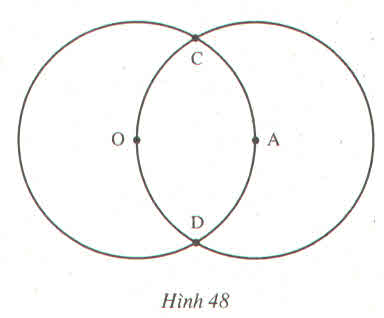
Trên hình 48, ta có hai đường tròn (0;2cm) và (A; 2cm) cắt nhau tại C, D. Điểm A nằm trên đường tròn tâm O
a) Vẽ đường tròn tâm C, bán kính 2cm ?
b) Vì sao đường tròn (C; 2cm) đi qua O, A ?
Trên hình 49, ta có hai đường tròn (A; 3cm) và (B; 2cm) cắt nhau tại C, D, AB = 4cm. Đường tròn A, B lần lượt cắt đoạn AB tại K, I
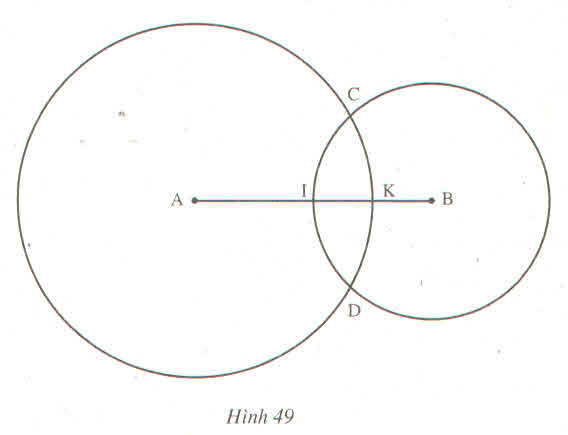
a) Tính CA, CB, DA, DB ?
b) I có phải là trung điểm của đoạn thẳng AB không ?
c) Tính IK ?
Giải:
a) CA=2cm; DA= 3cm; CB= 2cm; DB= 2cm
b) Điểm I nằm giữa A và B nên
AI+ IB= AB= 4cm.
Mặt khác, IB= 2cm
Nên AI= 4 - 2 =2cm.
Vậy AI=IB(=2cm) suy ra I là trung điểm của AB.
c) Điểm I nằm giữa A và K nên
AI+ IK= AK,
Suy ra IK=AK-AI= 3-2 =1 cm.
Trả lời bởi Thien Tu Borum
Đố :
Xem hình 51, so sánh AB + BC + AC với OM bằng mắt rồi kiểm tra bằng dụng cụ ?
Giải:
Trên tia OM kể từ O ta đặt liên tiếp ba đoạn thẳng có độ dài lần lượt bằng AB,BC,CA. Ta thấy điểm cuối trùng với M.
Vậy AB + BC + CA= OM.
Trả lời bởi Thien Tu BorumVẽ lại cách hình sau (đúng kích thước như hình đã cho) :
Hướng dẫn vẽ:
a) Trước hết vẽ đường tròn bán kính 1.2 cm rồi vẽ đường kình của đường tròn. Trên hai nửa mặt phẳng bờ đối nhau là đường kính vẽ hai nửa đường tròn có đường kính lần lượt là đoạn nối tâm tới một đầu của đường kính vừa vẽ. Sau cùng tô màu như hình vẽ.
b) Trước hết, vẽ hình vuông. Lấy giao điểm của hai đường chéo làm tâm vẽ 5 đường tròn có bán kính lần lượt bằng bán kính của 5 đường tròn đã cho.
c) Trước hết vẽ đường tròn ở chính giữa có bán kình R. Vẽ một đường tròn phụ trùng với tâm đường tròn vừa vẽ, bán kính 2 R. Trên đường tròn phụ, vẽ liên tiếp 6 dây, mỗi dây có độ dài 2R .Sau đó vẽ sáu đường tròn có tâm là mút của mỗi dây.
d) Vẽ đường tròn bán kính R bằng bán kình của đường tròn ở chính giữa. Vẽ liên tiếp sáu dây, mỗi dây dài R. Vẽ sáu nửa đường tròn ra phía ngoài của đường tròn vừa vẽ mỗi nửa đường tròn có đường kính là mỗi dây.
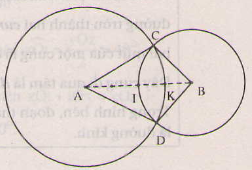
Trả lời bởi Thien Tu BorumCho hai điểm A, B cách nhau 3cm. Vẽ đường tròn (A; 2,5cm) và đường tròn (B; 1,5cm). Hai đường tròn này cắt nhau tại C và D
a) Tính CA, DB
b) Tại sao đường tròn (B; 1,5cm) cắt đoạn thẳng AB tại trung điểm I của AB ?
c) Đường tròn (A; 2,5cm) cắt đoạn thẳng AB tại K. Tính KB ?
(Mk vẽ không chính xác được)
a) Vì (A) cắt (B) tại C và D nên :
- Điểm D nằm trên đường tròn tâm A \(\Rightarrow\) AD là bán kính của hình tròn tâm A nên AD = 2,5cm
- Điểm D nằm trên đường tròn tâm B \(\Rightarrow\) DB là bán kính của hình tròn tâm B nên DB = 1,5 cm
b) Vì đường tròn tâm B cắt AB tại I nên I nằm giữa 2 điểm AB (1)
Ta có : Điểm I nằm trên đường tròn tâm B nên IB = bán kính của hình tròn tâm B = 1,5 cm
\(\Rightarrow\) AI + IB = AB hay AI = AB - IB = 3 - 1,5 - 1,5 (cm) (2)
Từ (1) và (2) \(\Rightarrow\) Đường tròn tâm B cắt AB tại trung điểm I của AB
c) Vì đường tròn tâm A cắt AB tại K nên K nằm giữa 2 điểm AB
Ta có : Điểm K nằm trên đường tròn tâm A nên AK = bán kính của hình tròn tâm A = 2,5 cm
\(\Rightarrow\) KB + AK = AB hay KB = AB - AK = 3 - 2,5 = 0,5 (cm)
Trả lời bởi Lê Tuấn Nghĩa
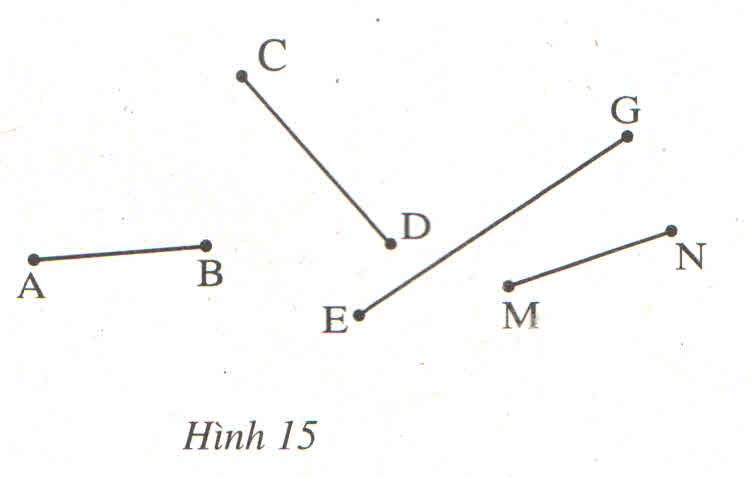
So sánh các đoạn thẳng trong hình 15 bằng mắt rồi kiểm trả kết quả bằng compa ?
Làm thế nào để chỉ đo một lần, mà biết được tổng độ dài các đoạn thẳng ở hình 16 ?
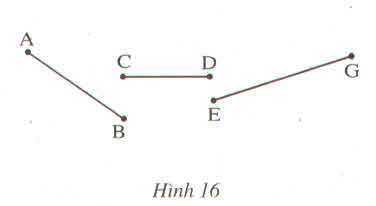
Muốn biết tổng độ dài các đoạn thẳng ở hình 16 trong 1 lần đo , ta dùng compa ''chuyển '' các đoạn thẳng AB ; CD; EG lên một đường thẳng sao cho mút C trùng mút B , mút E trùng mút D . Đo đoạn thẳng EG ta có :
AG = AB + CD + EG = 6 cm
Vậy tổng độ dài ba đoạn thẳng đó là 6 cm
Trả lời bởi Mai Hà Chia) Vẽ đoạn thẳng AB bằng 3cm
b) Vẽ đường tròn tâm A bán kính 2 cm
c) Vẽ đường tròn tâm B bán kính 2cm
d) Đặt tên giao điểm của hai đường tròn là C, D
e) Vẽ đoạn thẳng CD
g) Đặt tên giao điểm của AB và CD là I
h) Đo IA và IB
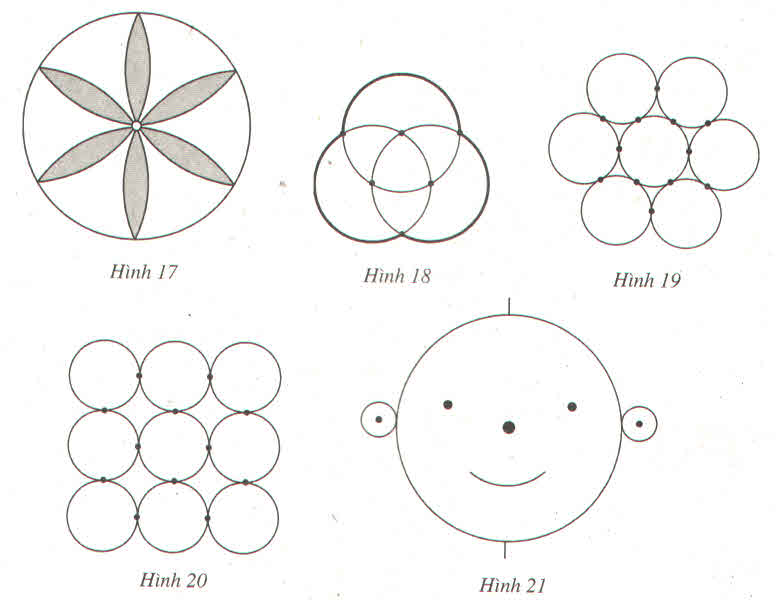
Vẽ lại các hình sau (đúng kích thước như hình đã cho : hình 17, 18, 19, 20, 21)
Vẽ hình liên tiếp theo các cách diễn đạt sau :
a) Vẽ đoạn thẳng AB = 2cm. Vẽ đường tròn (\(C_1\)) tâm A, bán kính AB
b) Vẽ đường tròn \(\left(C_2\right)\) tâm B, bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn \(\left(C_1\right)\) là C và G
c) Vẽ đường tròn \(\left(C_3\right)\) tâm C, bán kính AC. Gọi các giao điểm mới của đường tròn này với đường tròn \(\left(C_1\right)\) là D
d) Vẽ đường tròn \(\left(C_4\right)\) tâm D, bán kính AD. Gọi các giao điểm mới của đường tròn này với đường tròn \(\left(C_1\right)\) là E
e) Vẽ đường tròn \(\left(C_5\right)\) tâm E, bán kính AE. Gọi các giao điểm mới của đường tròn này với đường tròn \(\left(C_1\right)\) là F
f) Vẽ đường tròn \(\left(C_6\right)\) tâm F, bán kính AF.
g) Vẽ đường tròn \(\left(C_7\right)\) tâm G, bán kính AG
Sau khi vẽ như trên, hãy so sánh các đoạn thẳng AB, BC, CD, DE, EF, FG, GB
Giải:
a) Xem hình bên
b) Đường tròn (C;2cm) đi qua O và A vì O và A cách C là 2cm.
Trả lời bởi Thien Tu Borum