Trong hệ thập phân, mỗi số có thể được phân tích thành tổng các luỹ thừa của 10 với hệ số của mỗi số hạng chính là các chữ số tương ứng của số đó. Ví dụ số 513 có thể viết thành: 5 x 102 + 1 x 101 + 3 x 100
Ta cũng có thể phân tích một số thành tổng các luỹ thừa của 2, chẳng hạn 13 có thể viết thành: 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 với các hệ số chỉ là 0 hoặc 1
Khi đó, có thể thể hiện 13 bởi 1101 được không? Em hãy cho biết việc thể hiện giá trị của một số bằng dãy bit có lợi gì.
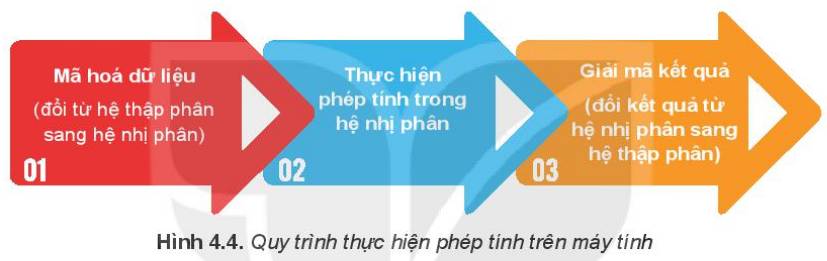
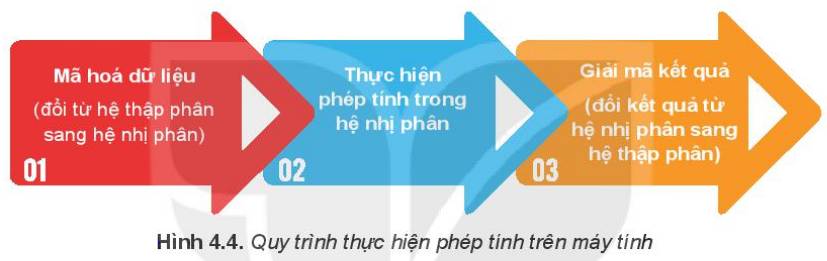
Khi đó,có thể thể hiện 13 bởi 1101 được
Việc thể hiện giá trị của một số bằng dãy bit có lợi là giúp biểu diễn được con số trong máy tính
Trả lời bởi 𝓗â𝓷𝓷𝓷