Hai vách ngăn tủ trong Hình 45 gợi nên hình ảnh hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cắt nhau tạo nên bốn góc nhị diện. Các góc nhị diện đó có phải là những góc nhị diện vuông hay không?
Nêu ví dụ trong thực tiễn minh hoạ hình ảnh hai mặt phẳng vuông góc.
Những ví dụ trong thực tiễn minh hoạ hình ảnh hai mặt phẳng vuông góc là: Mặt tường vuông góc với sàn nhà, mặt ngang vuông góc với mặt đứng của bậc thang,…
Trả lời bởi Quoc Tran Anh LeNền nhà, cánh cửa và mép cánh cửa ở Hình 48 gợi nên hình ảnh mặt mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) và đường thẳng \(a\) nằm trên mặt phẳng \(\left( P \right)\). Quan sát Hình 48 và cho biết:
a) Vị trí tương đối của đường thẳng \(a\) và mặt phẳng \(\left( Q \right)\);
b) Hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) có vuông góc với nhau không.
a: \(a\perp\left(Q\right)\)
b: Hai mặt phẳng (P) và (Q) có vuông góc với nhau
Trả lời bởi Nguyễn Lê Phước ThịnhCho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(SA \bot \left( {ABCD} \right)\). Chứng minh rằng \(\left( {SAC} \right) \bot \left( {SBD} \right)\).
\(ABCD\) là hình thoi \( \Rightarrow AC \bot B{\rm{D}}\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot B{\rm{D}}\)
\(\left. \begin{array}{l} \Rightarrow B{\rm{D}} \bot \left( {SAC} \right)\\B{\rm{D}} \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow \left( {SAC} \right) \bot \left( {SB{\rm{D}}} \right)\)
Trả lời bởi Hà Quang MinhCho hình chóp \(S.OAB\) thoả mãn \(\left( {AOS} \right) \bot \left( {AOB} \right)\), \(\widehat {AOS} = \widehat {AOB} = {90^ \circ }\) (Hình 51).
a) Giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\) là đường thẳng nào?
b) \(SO\) có vuông góc với giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\) hay không?
c) \(SO\) có vuông góc với mặt phẳng \(\left( {AOB} \right)\) hay không?
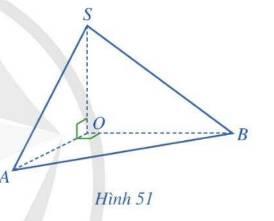
a) Ta có:
\(\left. \begin{array}{l}A \in \left( {AOS} \right) \cap \left( {AOB} \right)\\O \in \left( {AOS} \right) \cap \left( {AOB} \right)\end{array} \right\} \Rightarrow AO = \left( {AOS} \right) \cap \left( {AOB} \right)\)
b) \(\widehat {AOS} = {90^ \circ } \Rightarrow SO \bot AO\)
Vậy \(SO\) có vuông góc với giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\).
c) \(\widehat {AOS} = {90^ \circ } \Rightarrow SO \bot AO\)
\(\widehat {AOB} = {90^ \circ } \Rightarrow AO \bot BO\)
Vậy \(\widehat {SOB}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {S,AO,B} \right]\)
Vì \(\left( {AOS} \right) \bot \left( {AOB} \right)\) nên \(\widehat {SOB} = {90^ \circ }\)
\(\left. \begin{array}{l} \Rightarrow SO \bot OB\\SO \bot OA\end{array} \right\} \Rightarrow SO \bot \left( {AOB} \right)\)
Trả lời bởi Quoc Tran Anh LeCho tứ diện \(ABCD\) có \(\left( {ABD} \right) \bot \left( {BCD} \right)\) và \(CD \bot BD\). Chứng minh rằng tam giác \(ACD\) vuông.
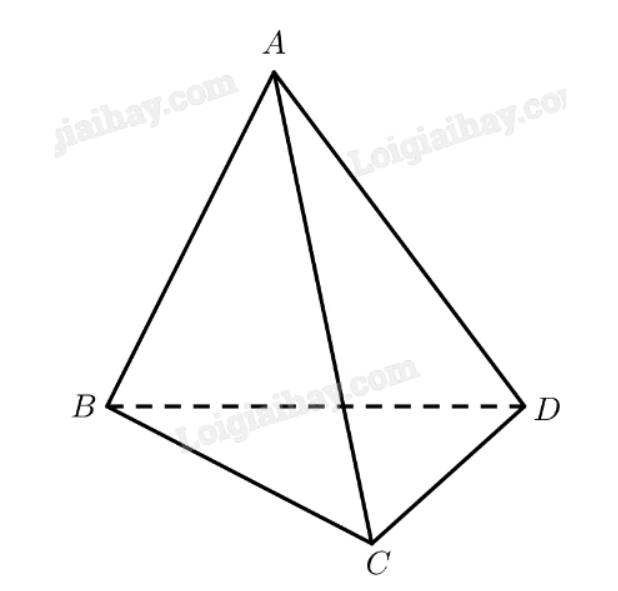
Ta có:
\(\left. \begin{array}{l}\left( {ABD} \right) \bot \left( {BCD} \right)\\\left( {ABD} \right) \cap \left( {BCD} \right) = BD\\C{\rm{D}} \subset \left( {BCD} \right)\\C{\rm{D}} \bot B{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABD} \right) \Rightarrow C{\rm{D}} \bot A{\rm{D}}\)
Vậy tam giác \(ACD\) vuông tại \(D\).
Trả lời bởi Quoc Tran Anh LeTrong Hình 54, hai bìa của cuốn sách gợi nên hình ảnh hai mặt phẳng vuông góc với mặt bàn. Hãy dự đoán xem gáy sách có vuông góc với mặt bàn hay không.
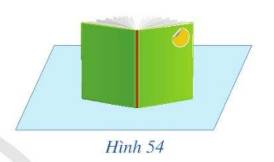
gáy sách có vuông góc với mặt bàn
Trả lời bởi Nguyễn Lê Phước ThịnhCho hình chóp \(S.ABC\) có \(SA \bot SB,SB \bot SC,SC \bot SA\). Chứng minh rằng:
a) \(\left( {SAB} \right) \bot \left( {SBC} \right)\);
b) \(\left( {SBC} \right) \bot \left( {SCA} \right)\);
c) \(\left( {SCA} \right) \bot \left( {SAB} \right)\).
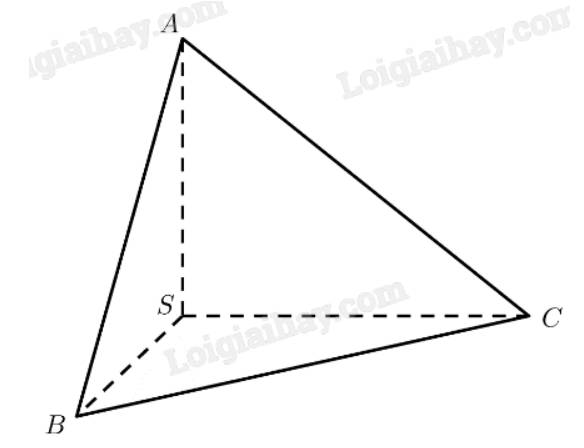
a) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}SA \bot SB\\SA \bot SC\end{array} \right\} \Rightarrow SA \bot \left( {SBC} \right)\\SA \subset \left( {SAB} \right)\end{array} \right\} \Rightarrow \left( {SAB} \right) \bot \left( {SBC} \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}SA \bot SB\\SA \bot SC\end{array} \right\} \Rightarrow SA \bot \left( {SBC} \right)\\SA \subset \left( {SCA} \right)\end{array} \right\} \Rightarrow \left( {SCA} \right) \bot \left( {SBC} \right)\)
c) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}SA \bot SB\\SB \bot SC\end{array} \right\} \Rightarrow SB \bot \left( {SCA} \right)\\SB \subset \left( {SAB} \right)\end{array} \right\} \Rightarrow \left( {SAB} \right) \bot \left( {SCA} \right)\)
Trả lời bởi Quoc Tran Anh LeQuan sát ba mặt phẳng \(\left( P \right),\left( Q \right),\left( R \right)\) ở Hình 57, chỉ ra hai cặp mặt phẳng mà mỗi cặp gồm hai mặt phẳng vuông góc với nhau. Hãy sử dụng kí hiệu để viết những kết quả đó.
\(\left(P\right)\perp\left(R\right);\left(Q\right)\perp\left(R\right)\)
Trả lời bởi Nguyễn Lê Phước ThịnhChứng minh định lí sau: Nếu hai mặt phẳng vuông góc với nhau thì mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
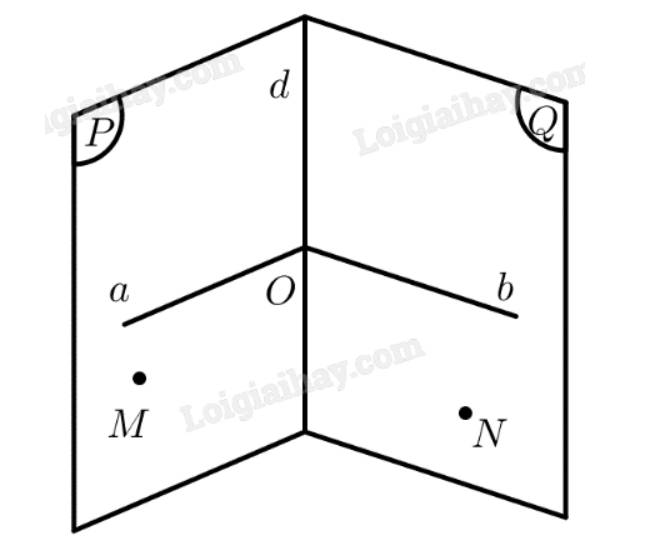
Cho hai mặt phẳng \(\left( P \right),\left( Q \right)\) vuông góc với nhau. Ta cần chứng minh tồn tại một đường thẳng \(a \subset \left( P \right)\) sao cho \(a \bot \left( Q \right)\).
Gọi \(d = \left( P \right) \cap \left( Q \right)\). Lấy \(M \in \left( P \right),N \in \left( Q \right)\) sao cho \(M,N \notin d\).
Gọi góc \(\widehat {aOb}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {M,d,N} \right]\).
Vì \(\left( P \right) \bot \left( Q \right)\) nên góc nhị diện đó là góc nhị diện vuông. Vậy \(\widehat {aOb} = {90^ \circ } \Rightarrow a \bot b\).
Mà \(a \bot d\)
\( \Rightarrow a \bot \left( Q \right)\)
Trả lời bởi Quoc Tran Anh Le
Các góc nhị diện đó là các góc nhị diện vuông
Trả lời bởi Nguyễn Lê Phước Thịnh