Báo đốm (hình 3.1) có tốc độ tối đa khoảng 30 m/s. Từ lúc đứng yên, sau một vài bước nhảy, một con báo đốm có thể đạt tốc độ 20 m/s chỉ sau 2 s.
Một ô tô tăng tốc từ lúc đứng yên, sau 6,0 s đạt vận tốc 18 m/s. Tính độ lớn gia tốc của ô tô.
\(t_o=0s\rightarrow v_o=0\)(m/s)
\(t=6s\rightarrow v=18\) (m/s)
\(a=\dfrac{\Delta v}{\Delta t}=\dfrac{v-v_o}{t-t_o}=\dfrac{18-0}{6-0}=3m\)/\(s^2\)
Trả lời bởi YangSuNgười lái xe ô tô hãm phanh để xe giảm tốc độ từ 23 m/s đến 11 m/s trong 20 s. Tính độ lớn của gia tốc.
\(a=\dfrac{\Delta v}{\Delta t}=\dfrac{11-23}{20}=-0,6\left(\dfrac{m}{s^2}\right)\)
Trả lời bởi GV Nguyễn Trần Thành ĐạtTrong một cuộc thi chạy, từ trạng thái đứng yên, một vận động viên chạy với gia tốc 5,0 m/s2 trong 2,0 giây đầu tiên. Tính vận tốc của vận động viên sau 2,0 s.
Một người lái ô tô đang đi với tốc độ ổn định trên đường cao tốc, chợt nhìn thấy tín hiệu báo có nguy hiểm ở phía trước nên dần dần giảm tốc độ. Ô tô tiến thêm một đoạn thì người này thấy một tai nạn đã xảy ra và phanh gấp để dừng lại. Vẽ phác đồ thị vận tốc – thời gian để biểu diễn chuyển động của ô tô này.
Từ độ dốc của đồ thị vận tốc – thời gian của chuyển động thẳng trên hình 3.3, hình nào tương ứng với mỗi phát biểu sau đây?
1. Độ dốc dương, gia tốc không đổi.
2. Độ dốc lớn hơn, gia tốc lớn hơn.
3. Độ dốc bằng không, gia tốc a = 0.
4. Độ dốc âm, gia tốc âm (chuyển động chậm dần).
Bảng 3.2 liệt kê một số giá trị vận tốc của người đi xe máy trong quá trình tốc độ dọc theo một con đường thẳng.
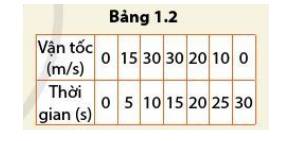
a) Vẽ đồ thị vận tốc – thời gian cho chuyển động này.
b) Từ những số đo trong bảng, hãy suy nghĩ gia tốc của người đi xe máy trong 10 s đầu tiên.
c) Kiểm tra kết quả tính được của bạn bằng cách tìm độ dốc của đồ thị trong 10 s đầu tiên.
d) Xác định gia tốc của người đi xe máy trong thời gian 15 s cuối cùng.
e) Sử dụng đồ thị để tìm tổng quãng đường đã đi trong quá trình thử tốc độ.
a)
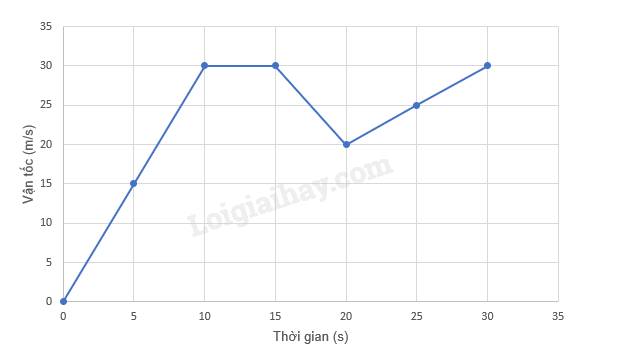
b)
Trong 10 s đầu tiên, ta có:
+ \(\Delta v = 30(m/s)\)
+ \(\Delta t = 10(s)\)
=> Gia tốc của người đi xe máy trong 10 s đầu tiên là:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{30}}{{10}} = 3(m/{s^2})\)
c) Từ đồ thị ta có:
+ \(\Delta v = 30(m/s)\)
+ \(\Delta t = 10(s)\)
=> Độ dốc của người đi xe máy trong 10 s đầu tiên là:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{30}}{{10}} = 3(m/{s^2})\)
d) Trong 15 s cuối cùng, ta có:
+ \(\Delta v = 30(m/s)\)
+ \(\Delta t = 15(s)\)
=> Gia tốc của người đi xe máy trong 15 s cuối cùng là:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{30}}{{15}} = 2(m/{s^2})\)
e) Do vật không đổi chiều chuyển động nên độ dịch chuyển = quãng đường đi được = Diện tích đồ thị
+ Từ 0 - 10 s, quãng đường vật đi được là: \({S_1} = \frac{1}{2}.10.30 = 150(m)\)
+ Từ 10 - 15 s, quãng đường vật đi được là: \({S_2} = 30.5 = 150(m)\)
+ Từ 15 s - 20 s, quãng đường vật đi được là: \({S_3} = \frac{{(30 + 20).5}}{2} = 125(m)\)
+ Từ 20 s - 30 s, quãng đường vật đi được là: \({S_4} = \frac{{(30 + 20).10}}{2} = 250(m)\)
=> Tổng quãng đường vật đi được là: S = 150 + 150 + 125 + 250 = 675 (m).
Trả lời bởi Quoc Tran Anh LeĐồ thị vận tốc – thời gian (hình 3.7) biểu diễn chuyển động thẳng của ô tô trong khoảng thời gian 30 s.
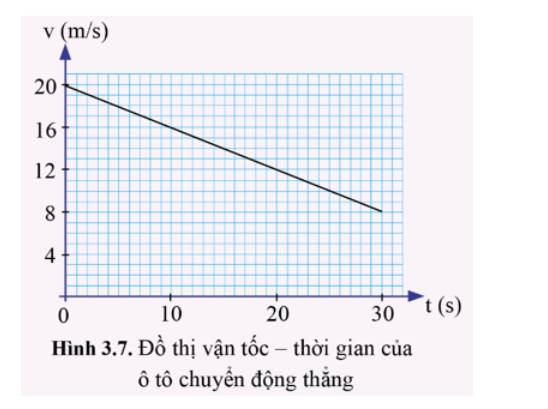
a) Mô tả chuyển động của ô tô.
b) Từ đồ thị, xác định vận tốc ban đầu và vận tốc cuối cùng của ô tô trong thời gian 30 s.
c) Xác định gia tốc a của ô tô.
d) Bằng cách tính diện tích dưới đồ thị, hãy xác định độ dịch chuyển của ô tô.
e) Tính độ dịch chuyển của ô tô bằng công thức \(d=v_ot+\dfrac{1}{2}at^2\). So sánh với kết quả ở phần d.
Tăng tốc độ là sự thay đổi tốc độ của chuyển động từ giá trị nhỏ đến giá trị lớn trong một khoảng thời gian nào đó.
Trả lời bởi Quoc Tran Anh Le