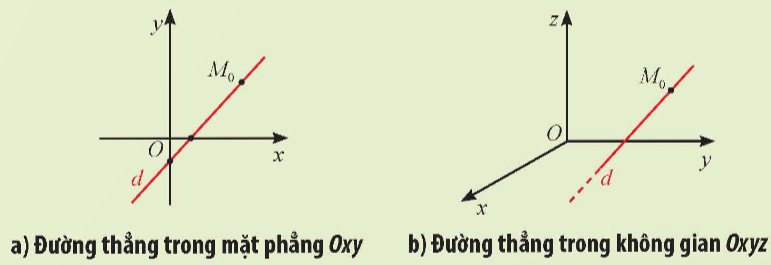
Ta đã biết trong mặt phẳng Oxy, phương trình tham số của đường thẳng có dạng:
\(\left\{{}\begin{matrix}x=x_0+a_1t\\y=y_0+a_2t\end{matrix}\right.\left(a_1^2+a^2_2\ne0,t\in R\right)\).
Trong không gian Oxyz, phương trình tham số của đường thẳng có dạng như thế nào?.
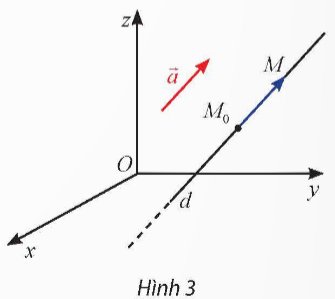
Trong không gian Oxyz, phương trình tham số của đường thẳng d đi qua điểm $\mathrm{M}_0\left(\mathrm{x}_0 ; \mathrm{y}_0 ; \mathrm{z}_0\right)$ và nhận $\vec{a}=\left(a_1 ; a_2 ; a_3\right)$ làm vectơ chỉ phương có dạng: $\left\{\begin{array}{l}x=x_0+a_1 t \\ y=y_0+a_2 t \text { với } \mathrm{t} \in \mathbb{R} \text { (t được gọi là tham số). } \\ z=z_0+a_3 t\end{array}\right.$
Trả lời bởi datcoder