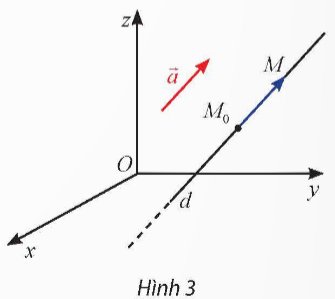
Trong không gian Oxyz, cho đường thẳng d đi qua điểm M0(x0; y0; z0) cố định và có vectơ chỉ phương là \(\overrightarrow{a}=\left(a_1;a_2;a_3\right)\) khác \(\overrightarrow{0}\).
a) Giải thích tại sao có thể viết: \(M\in d\Leftrightarrow\overrightarrow{M_0M}=t\overrightarrow{a}\left(t\in R\right)\).
b) Với M(x; y; z) thuộc d, hãy tính x, y, z theo x0, y0, z0 và a1, a2, a3.
a) Ta có \(\vec a\) là vectơ chỉ phương của đường thẳng \(d\).
Nếu \(M \in d\), ta có \(d\) đi qua hai điểm \(M\) và \({M_0}\) nên hai vectơ \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương, suy ra \(\overrightarrow {{M_0}M} = t\vec a\) với \(t \in \mathbb{R}\).
Ngược lại, với \(\overrightarrow {{M_0}M} = t\vec a\) thì \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương. Mà \(\vec a\) là vectơ chỉ phương của đường thẳng \(d\), nên \(\overrightarrow {{M_0}M} \) cũng là một vectơ chỉ phương của đường thẳng \(d\). Do \({M_0} \in d\), nên ta suy ra \(M \in d\).
b) Ta có \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\) và \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\).
Theo câu a, ta có \(\overrightarrow {{M_0}M} = t\vec a\) nên \(\left( {x - {x_0};y - {y_0};z - {z_0}} \right) = t\left( {{a_1};{a_2};{a_3}} \right)\)
Suy ra \(\left\{ \begin{array}{l}x - {x_0} = t{a_1}\\y - {y_0} = t{a_2}\\z - {z_0} = t{a_3}\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = {x_0} + t{a_1}\\y = {y_0} + t{a_2}\\z = {z_0} + t{a_3}\end{array} \right.\)

