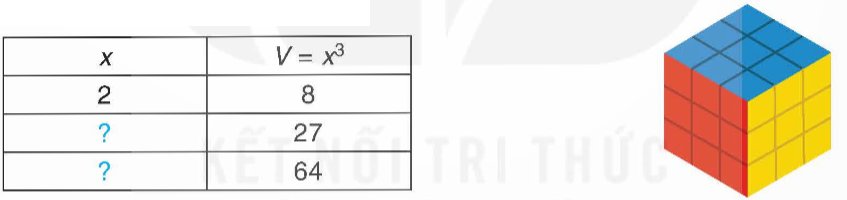
Kí hiệu V là thể tích của hình lập phương với cạnh x. Hãy thay dấu “?” trong bảng sau bằng các giá trị thích hợp.
Kí hiệu V là thể tích của hình lập phương với cạnh x. Hãy thay dấu “?” trong bảng sau bằng các giá trị thích hợp.

Tính: a) \(\sqrt[3]{125}\); b) \(\sqrt[3]{0,008}\); c) \(\sqrt[3]{\dfrac{-8}{27}}\).
a) \(\sqrt[3]{{125}} = 5\)
b) \(\sqrt[3]{{0,008}} = 0,2\)
c) \(\sqrt[3]{{\frac{{ - 8}}{{27}}}} = \frac{{ - 2}}{3}\)
Trả lời bởi datcoderSử dụng MTCT, tính \(\sqrt[3]{45}\) và làm tròn kết quả với độ chính xác 0,005.
Bấm các phím ![]() , màn hình hiện kết quả 3,556893304.
, màn hình hiện kết quả 3,556893304.
Làm tròn kết quả với độ chính xác 0,005 (tức là làm tròn kết quả đến chữ số thập phân thứ hai), ta được \(\sqrt[3]{46}\approx3,56\)
Trả lời bởi datcoderCó thể xếp 125 khối lập phương đơn vị (có cạnh bằng 1 cm) thành một khối lập phương lớn được không nhỉ?
Thể tích của khối lập phương đơn vị là \({1^3} = 1\left( {c{m^3}} \right)\)
Do đó thể tích của 125 khối lập phương là \(125.1 = 125\left( {c{m^3}} \right)\)
Giả sử xếp được 125 khối lập phương thành khối lập phương lớn cạnh là x cm, thì ta có thể tích của hình lập phương mới là \({x^3}\left( {c{m^3}} \right)\)
Từ đó ta có \({x^3} = 125\) hay \(x = 5\)
Vậy ta có thể xếp được 125 khối lập phương đơn vị thành một khối lập phương mới cạnh là 5 cm.
Trả lời bởi datcodera) Tính giá trị của căn thức \(\sqrt[3]{5x-1}\) tại x = 0 và tại x = –1,4.
b) Rút gọn biểu thức \(\sqrt[3]{x^3-3x^2+3x-1}\).
a) Tại \(x = 0\) ta có \(\sqrt[3]{{5.0 - 1}} = \sqrt[3]{{ - 1}} = - 1\)
Tại \(x = - 1,4\) ta có \(\sqrt[3]{{5.\left( { - 1,4} \right) - 1}} = \sqrt[3]{{ - 8}} = - 2\)
b) Ta có \(\sqrt[3]{{{x^3} - 3{x^2} + 3x - 1}} = \sqrt[3]{{{{\left( {x - 1} \right)}^3}}} = x - 1\)
Trả lời bởi datcoderTính:
a) \(\sqrt[3]{216}\); b) \(\sqrt[3]{-512}\); c) \(\sqrt[3]{-0,001}\); d) \(\sqrt[3]{1,331}\).
a) \(\sqrt[3]{{216}} = \sqrt[3]{{{6^3}}} = 6\)
b) \(\sqrt[3]{{ - 512}} = \sqrt[3]{{ - {8^3}}} = - 8\)
c) \(\sqrt[3]{{ - 0,001}} = \sqrt[3]{{ - {{\left( {0,1} \right)}^3}}} = - 0,1\)
d) \(\sqrt[3]{{1,331}} = \sqrt[3]{{1,{1^3}}} = 1,1\)
Trả lời bởi datcoderSử dụng MTCT, tính các căn bậc ba sau đây (làm tròn kết quả đến chữ số thập phân thứ hai):
a) \(\sqrt[3]{2,1}\); b) \(\sqrt[3]{-18}\); c) \(\sqrt[3]{-28}\); d) \(\sqrt[3]{0,35}\).
Một người thợ muốn làm một thùng tôn hình lập phương có thể tích bằng 730 dm3. Em hãy ước lượng chiều dài cạnh thùng khoảng bao nhiêu decimét.
Gọi chiều dài cạnh thùng là x (dm) (x > 0).
Thể tích hình lập phương là \(730dm^3\) nên ta có phương trình:
\(x^3 = 730\)
\(x= \sqrt[3]{730}\)
\(x \approx {9} (dm)\) (TM)
Vậy cạnh thùng khoảng 9dm.
Trả lời bởi datcoderRút gọn các biểu thức sau:
a) \(\sqrt[3]{\left(1-\sqrt{2}\right)^3}\); b) \(\sqrt[3]{\left(2\sqrt{2}+1\right)^3}\); c) \(\left(\sqrt[3]{\sqrt{2}+1}\right)^3\).
a) \(\sqrt[3]{{{{\left( {1 - \sqrt 2 } \right)}^3}}} = 1 - \sqrt 2 \)
b) \(\sqrt[3]{{{{\left( {2\sqrt 2 + 1} \right)}^3}}} = 2\sqrt 2 + 1\)
c) \({\left( {\sqrt[3]{{\sqrt 2 + 1}}} \right)^3} = \sqrt 2 + 1\)
Trả lời bởi datcoderRút gọn rồi tính giá trị của biểu thức \(\sqrt[3]{27x^3-27x^2+9x-1}\) tại x = 7.
Ta có \(\sqrt[3]{{27{x^3} - 27{x^2} + 9x - 1}} = \sqrt[3]{{{{\left( {3x - 1} \right)}^3}}} = 3x - 1\)
Tại \(x = 7\) ta có \(3.7 - 1 = 20\)
Vậy tại \(x = 7\) biểu thức có giá trị bằng 20.
Trả lời bởi datcoder
Ta có:
⦁ x3 = 27 hay x3 = 33, suy ra x = 3.
⦁ x3 = 64 hay x3 = 43, suy ra x = 4.
Vậy ta hoàn thành được bảng trên như sau:
x
V = x3
2
8
3
27
4
64