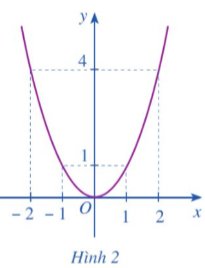
Một doanh nghiệp dự kiến lợi nhuận khi sản xuất x sản phẩm (0 ≤ x ≤ 300) được cho bởi hàm số y = – x3 + 300x2 (đơn vị: nghìn đồng) và được minh họa bằng đồ thị ở Hình 1.

Sự thay đổi lợi nhuận theo số sản phẩm sản xuất ra và dấu của đạo hàm y' có mối liên hệ với nhau như thế nào?





Ta có y = – x3 + 300x2 với x ∈ [0; 300].
y' = – 3x2 + 600x;
y' = 0 ⇔ x = 0 hoặc x = 200.
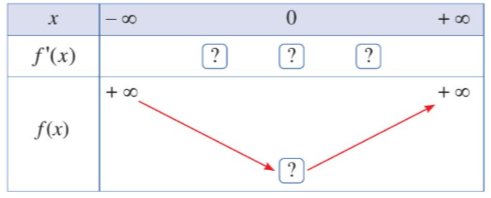
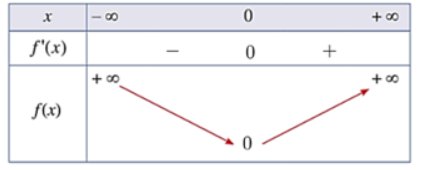
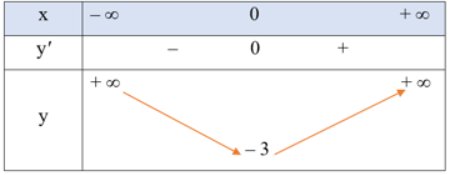
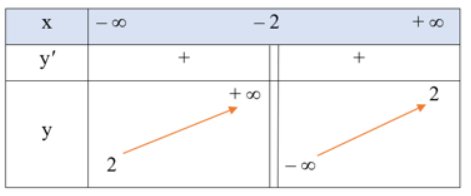
Bảng xét dấu của y' trên đoạn [0; 300] như sau:
Kết hợp với đồ thị ở Hình 1, ta thấy lợi nhuận theo số sản phẩm sản xuất ra tăng thì đạo hàm y' mang dấu dương, lợi nhuận theo số sản phẩm sản xuất ra giảm thì đạo hàm y' mang dấu âm.
Trả lời bởi datcoder