Một đội công nhân làm đường nhận nhiệm vụ trải nhựa \(8100{m^2}\) mặt đường. Ở giai đoan đầu, đội trải được \(3600{m^2}\) mặt đường. Ở giai đoạn hai đội công nhân tăng năng suất thêm \(300{m^2}/\)ngày rồi hoàn thành công việc. Hỏi đội công nhân đã hoàn thành công việc trong bao nhiêu ngày? Biết rằng năng suất lao động của đội không thay đổi ở mỗi giai đoạn và thời gian làm việc của hai giai đoạn là như nhau.
Bài 1. Phương trình quy về phương trình bậc nhất một ẩn
HM
Một đội công nhân làm đường nhận nhiệm vụ trải nhựa 8100{m^2} mặt đường. Ở giai đoan đầu, đội trải được 3600{m^2} mặt đường. Ở giai đoạn hai đội công nhân tăng năng suất thêm 300{m^2}/ngày rồi hoàn thành công việc. Hỏi đội công nhân đã hoàn thành công việc trong bao nhiêu ngày? Biết rằng năng suất lao động của đội không thay đổi ở mỗi giai đoạn và thời gian làm việc của hai giai đoạn là như nhau.
Đọc tiếp
Hướng dẫn giải
Thảo luận (1)
HM
Giải các phương trình:
a. \(\left( {9x - 4} \right)\left( {2x + 5} \right) = 0\);
b. \(\left( {1,3x + 0,26} \right)\left( {0,2x - 4} \right) = 0\);
c. \(2x\left( {x + 3} \right) - 5\left( {x + 3} \right) = 0\);
d. \({x^2} - 4 + \left( {x + 2} \right)\left( {2x - 1} \right) = 0\).
Hướng dẫn giải
Thảo luận (1)
a. \(\left( {9x - 4} \right)\left( {2x + 5} \right) = 0\)
Để giải phương trình đã cho, ta giải hai phương trình sau:
*) \(9x - 4 = 0\)
\(x = \frac{4}{9}\);
*) \(2x + 5 = 0\)
\(x = - \frac{5}{2}\).
Vậy phương trình có nghiệm \(x = \frac{4}{9}\) và \(x = - \frac{5}{2}\).
b. \(\left( {1,3x + 0,26} \right)\left( {0,2x - 4} \right) = 0\)
Để giải phương trình đã cho, ta giải hai phương trình sau:
*) \(1,3x + 0,26 = 0\)
\(x = 0,2\);
*) \(0,2x - 4 = 0\)
\(x = 20\).
Vậy phương trình có nghiệm \(x = 0,2\) và \(x = 20\).
c. \(2x\left( {x + 3} \right) - 5\left( {x + 3} \right) = 0\)
\(\left( {2x - 5} \right)\left( {x + 3} \right) = 0\).
Để giải phương trình đã cho, ta giải hai phương trình sau:
*) \(2x - 5 = 0\)
\(x = \frac{5}{2}\);
*) \(x + 3 = 0\)
\(x = - 3\).
Vậy phương trình có nghiệm \(x = \frac{5}{2}\) và \(x = - 3\).
d. \({x^2} - 4 + \left( {x + 2} \right)\left( {2x - 1} \right) = 0\)
\(\left( {x - 2} \right)\left( {x + 2} \right) + \left( {x + 2} \right)\left( {2x - 1} \right) = 0\)
\(\left( {x + 2} \right)\left( {x - 2 + 2x - 1} \right) = 0\)
\(\left( {x + 2} \right)\left( {3x - 3} \right) = 0\)
Để giải phương trình đã cho, ta giải hai phương trình sau:
*) \(x + 2 = 0\)
\(x = - 2\);
*) \(3x - 3 = 0\)
\(x = 1\).
Vậy phương trình đã cho có nghiệm \(x = - 2\) và \(x = 1\).
Trả lời bởi Hà Quang Minh
HM
Cho phương trình: frac{{x + 2}}{x} frac{{x - 3}}{{x - 2}},,left( 1 right).Tìm điều kiện của x để cả hai mẫu thức có trong phương trình (1) là khác 0.Cho mẫu của cả hai phân thức rồi giải điều kiện.
Đọc tiếp
Cho phương trình: \(\frac{{x + 2}}{x} = \frac{{x - 3}}{{x - 2}}\,\,\left( 1 \right)\).
Tìm điều kiện của \(x\) để cả hai mẫu thức có trong phương trình (1) là khác 0.
Cho mẫu của cả hai phân thức rồi giải điều kiện.
Hướng dẫn giải
Thảo luận (1)
Để mẫu thức trong phương trình (1) khác 0.
\(\left\{ \begin{array}{l}x \ne 0\\x - 2 \ne 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x \ne 0\\x \ne 2\end{array} \right.\)
Vậy \(x \ne 0;x \ne 2\) thì mẫu thức trong phương trình (1) khác 0.
Trả lời bởi Hà Quang Minh
HM
Giải phương trình: \(\frac{x}{{x - 2}} + \frac{1}{{x - 3}} = \frac{2}{{\left( {2 - x} \right)\left( {x - 3} \right)}}\).
Hướng dẫn giải
Thảo luận (1)
Điều kiện xác định: \(x \ne 2\) và \(x \ne 3\)
\(\frac{x}{{x - 2}} + \frac{1}{{x - 3}} = \frac{2}{{\left( {2 - x} \right)\left( {x - 3} \right)}}\)
\(\begin{array}{l}\frac{{x\left( {x - 3} \right)}}{{\left( {x - 2} \right)\left( {x - 3} \right)}} + \frac{{x - 2}}{{\left( {x - 2} \right)\left( {x - 3} \right)}} = - \frac{2}{{\left( {x - 2} \right)\left( {x - 3} \right)}}\\\frac{{{x^2} - 3x}}{{\left( {x - 2} \right)\left( {x - 3} \right)}} + \frac{{x - 2}}{{\left( {x - 2} \right)\left( {x - 3} \right)}} = - \frac{2}{{\left( {x - 2} \right)\left( {x - 3} \right)}}\\{x^2} - 3x + x - 2 = - 2\\{x^2} - 2x - 2 + 2 = 0\\{x^2} - 2x = 0\end{array}\)
\(x\left( {x - 2} \right) = 0\).
Để giải phương trình trên, ta giải hai phương trình:
*) \(x = 0\). *)\(x - 2 = 0\)
\(x = 2\).
Ta thấy:
+ \(x = 0\) thỏa mãn điều kiện xác định của phương trình;
+ \(x = 2\) không thỏa mãn điều kiện xác định của phương trình.
Vậy phương trình đã cho có nghiệm \(x = 0\).
Trả lời bởi Hà Quang Minh
HM
Tìm điều kiện xác định của phương trình \(\frac{{x - 8}}{{x - 7}} = 8 + \frac{1}{{1 - x}}\).
Hướng dẫn giải
Thảo luận (1)
Điều kiện xác định của phương trình \(\frac{{x - 8}}{{x - 7}} = 8 + \frac{1}{{1 - x}}\) là \(x - 7 \ne 0\) và \(1 - x \ne 0\) hay \(x \ne 7\) và \(x \ne 1\).
Trả lời bởi Hà Quang Minh
HM
Giải các phương trình:
a. \({x^2} - 10x + 25 = 5\left( {x - 5} \right)\);
b. \(4{x^2} - 16 = 5\left( {x + 2} \right)\).
Hướng dẫn giải
Thảo luận (1)
a. \({x^2} - 10x + 25 = 5\left( {x - 5} \right)\)
Ta có: \({x^2} - 10x + 25 = 5\left( {x - 5} \right)\)
\(\begin{array}{l}{\left( {x - 5} \right)^2} = 5\left( {x - 5} \right)\\{\left( {x - 5} \right)^2} - 5\left( {x - 5} \right) = 0\\\left( {x - 5} \right)\left( {x - 5 - 5} \right) = 0\end{array}\)
\(\left( {x - 5} \right)\left( {x - 10} \right) = 0.\)
Để giải phương trình trên, ta giải hai phương trình sau:
*) \(x - 5 = 0\)
\(x = 5;\)
*) \(x - 10 = 0\)
\(x = 10.\)
Vậy phương trình đã cho có hai nghiệm là \(x = 5\) và \(x = 10\).
Trả lời bởi Hà Quang Minh
HM
a. Cho hai số thực u,v có tích uv 0. Có nhận xét gì về giá trị của u, v?b. Cho phương trình left( {x - 3} right)left( {2x + 1} right) 0.- Chứng tỏ rằng nghiệm của phương trình x - 3 0 và nghiêm của phương trình 2x + 1 0 đều là nghiệm của phương trình left( {x - 3} right)left( {2x + 1} right) 0.- Giả sử x {x_0} là nghiệm của phương trình left( {x - 3} right)left( {2x + 1} right) 0 . Giá trị x x_0^{} có phải là nghiệm của phương trình x - 3 0 hoặc phương trình 2x + 1 0 hay không?
Đọc tiếp
a. Cho hai số thực \(u,v\) có tích \(uv = 0\). Có nhận xét gì về giá trị của u, v?
b. Cho phương trình \(\left( {x - 3} \right)\left( {2x + 1} \right) = 0\).
- Chứng tỏ rằng nghiệm của phương trình \(x - 3 = 0\) và nghiêm của phương trình \(2x + 1 = 0\) đều là nghiệm của phương trình \(\left( {x - 3} \right)\left( {2x + 1} \right) = 0\).
- Giả sử \(x = {x_0}\) là nghiệm của phương trình \(\left( {x - 3} \right)\left( {2x + 1} \right) = 0\) . Giá trị \(x = x_0^{}\) có phải là nghiệm của phương trình \(x - 3 = 0\) hoặc phương trình \(2x + 1 = 0\) hay không?
Hướng dẫn giải
Thảo luận (1)
a. Nhận xét: u = 0 hoặc v = 0.
b.
Ý 1:
+ Ta có: \(x - 3 = 0 \Leftrightarrow x = 3\).
+ Ta có: \(2x + 1 = 0 \Leftrightarrow x = - \frac{1}{2}\).
Ý 2:
+ Thay \(x = 3\) vào phương trình \(\left( {x - 3} \right)\left( {2x + 1} \right) = 0\) ta được:
\(\left( {3 - 3} \right)\left( {2.3 + 1} \right) = 0 \Leftrightarrow 0.7 = 0 \Leftrightarrow 0 = 0\) (luôn đúng).
Vậy \(x = 3\) là nghiệm của phương trình \(\left( {x - 3} \right)\left( {2x + 1} \right) = 0\).
+ Thay \(x = - \frac{1}{2}\) vào phương trình \(\left( {x - 3} \right)\left( {2x + 1} \right) = 0\) ta được:
\(\left( { - \frac{1}{2} - 3} \right)\left[ {2.\left( { - \frac{1}{2}} \right) + 1} \right] = 0 \Leftrightarrow - \frac{7}{2}.0 = 0 \Leftrightarrow 0 = 0\) (luôn đúng).
Vậy \(x = - \frac{1}{2}\) là nghiệm của phương trình \(\left( {x - 3} \right)\left( {2x + 1} \right) = 0\).
Ý 3:
Khi \(x = x_0^{}\) là nghiệm của phương trình \(\left( {x - 3} \right)\left( {2x + 1} \right) = 0\) thì \(x = x_0^{}\) có là nghiệm của phương trình \(x - 3 = 0\) hoặc phương trình \(2x + 1 = 0\).
Trả lời bởi Hà Quang Minh
HM
Trong một khu đất có dạng hình vuông, người ta dành một mảnh đất có dạng hình chữ nhật ở góc khu đất làm bể bơi. Biết diện tích của bể bơi bằng \(1250{m^2}\). Độ dài cạnh của khu đất bằng bao nhiêu mét?
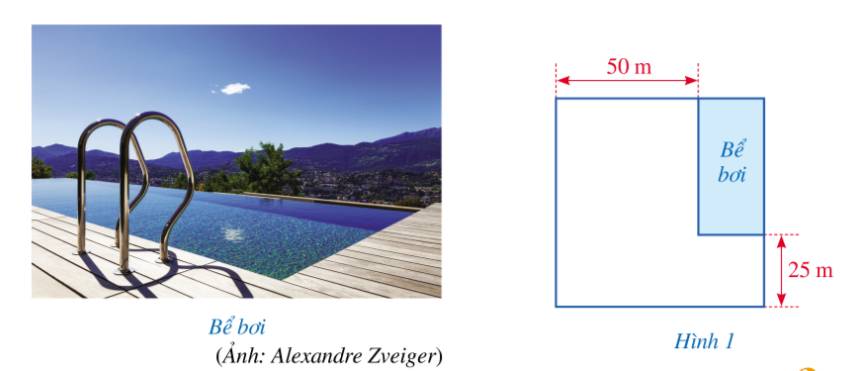
Hướng dẫn giải
Thảo luận (1)
+ Ta có: AE = 50m, GC = 25m, AB là độ dài cạnh khu đất cần tìm.
+ Ta có: AE = 50m, GC = 25m, AB là độ dài cạnh khu đất cần tìm.
+ Ta chia khu đất thành các hình:
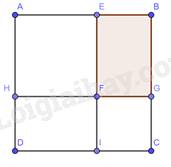
- Hình vuông AEFH, FGCI.
- Hình chữ nhật EBGF, HFID.
+ Ta có: IC = FG = EB = GC.
Suy ra AB = AE + EB = 50 + 25 = 75 (m).
Suy ra Độ dài cạnh khu đất cần tìm là: 75m.
Trả lời bởi Hà Quang Minh
HM
Giải phương trình: \(\left( {4x + 5} \right)\left( {3x - 2} \right) = 0\).
Hướng dẫn giải
Thảo luận (1)
Để giải phương trình trên ta giải hai phương trình sau:
*)\(4x + 5 = 0\)
\(x = - \frac{5}{4}\);
*)\(3x - 2 = 0\)
\(x = \frac{2}{3}\).
Vậy phương trình đã cho có hai nghiệm là \(x = - \frac{5}{4}\) và \(x = \frac{2}{3}\).
Trả lời bởi Hà Quang Minh
HM
Cho phương trình: frac{{2x + 1}}{{2x}} 1 - frac{2}{{x - 3}},,,left( 2 right)Hãy giả phương trình (2) theo các bước sau:a. Tìm điều kiện xác định của phương trình (2).b. Tìm mẫu thức chung, quy đồng mẫu thức các phân thức ở hai vế của phương trình (2) và khử mẫu.c. Giải phương trình vừa tìm được.d. Kiểm tra điều kiện xác định của phương trình (2) đối với các giá trị của ẩn vừa tìm được rồi kết luận.
Đọc tiếp
Cho phương trình: \(\frac{{2x + 1}}{{2x}} = 1 - \frac{2}{{x - 3}}\,\,\,\left( 2 \right)\)
Hãy giả phương trình (2) theo các bước sau:
a. Tìm điều kiện xác định của phương trình (2).
b. Tìm mẫu thức chung, quy đồng mẫu thức các phân thức ở hai vế của phương trình (2) và khử mẫu.
c. Giải phương trình vừa tìm được.
d. Kiểm tra điều kiện xác định của phương trình (2) đối với các giá trị của ẩn vừa tìm được rồi kết luận.
Hướng dẫn giải
Thảo luận (1)
a. Điều kiện xác định của phương trình \(\frac{{2x + 1}}{{2x}} = 1 - \frac{2}{{x - 3}}\) là \(2x \ne 0\) và \(x - 3 \ne 0\) hay \(x \ne 0\) và \(x \ne 3\).
b.
+ Mẫu thức chung của phương trình là: \(2x\left( {x - 3} \right)\).
+ Quy đồng mẫu thức: \(\frac{{\left( {2x + 1} \right)\left( {x - 3} \right)}}{{2x\left( {x - 3} \right)}} = \frac{{2x\left( {x - 3} \right)}}{{2x\left( {x - 3} \right)}} - \frac{{4x}}{{2x\left( {x - 3} \right)}}\).
+ Khử mẫu: \(\left( {2x + 1} \right)\left( {x - 3} \right) = 2x\left( {x - 3} \right) - 4x\).
c. Giải phương trình:\(\left( {2x + 1} \right)\left( {x - 3} \right) = 2x\left( {x - 3} \right) - 4x\).
\(\begin{array}{l}2{x^2} - 6x + x - 3 = 2{x^2} - 6x - 4x\\2{x^2} - 6x + x - 3 - 2{x^2} + 6x + 4x = 0\\5x - 3 = 0\end{array}\)
\(x = \frac{3}{5}\).
d. Ta thấy \(x = \frac{3}{5}\) thỏa mãn điều kiện xác định của phương trình.
Trả lời bởi Hà Quang Minh
Gọi số ngày đội công nhân hoàn thành công việc là: x (ngày, x > 0).
Thời gian làm việc của đội ở mỗi giai đoạn là: \(\frac{x}{2}\) (ngày).
Năng suất lao động của đội ở giai đoạn 1 là: \(3600:\frac{x}{2} = 7200x\) (\(m^2\)/ngày).
Giai đoạn 2 đội trải được: \(8100 - 3600 = 4500\left( {{m^2}} \right)\)
Năng suất lao động của đội ở giai đoạn 2 là: \(4500:\frac{x}{2} = 9000x\) (\(m^2\)/ngày).
Do giai đoạn hai, đội công nhân tăng năng suất thêm \(300\) (\(m^2\)/ngày). Ta có phương trình:
\(9000x - 7200x = 300\).
Giải phương trình: \(9000x - 7200x = 300\)
\(1800x = 300\)
\(x = \frac{1}{6}\) (thỏa mãn điều kiện x > 0).
Vậy đội công nhân hoàn thành công việc trong \(\frac{1}{6}\) ngày.
Trả lời bởi Hà Quang Minh