Một chiếc bánh lái tàu có thể quay theo cả hai chiều. Trong Hình 1 và Hình 2, lúc đầu thanh OM ở vị trí OA.
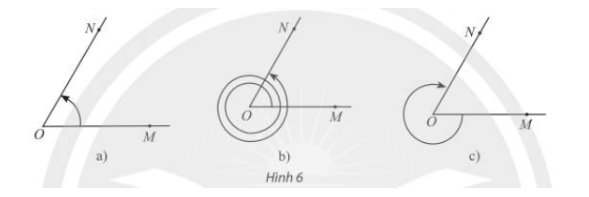
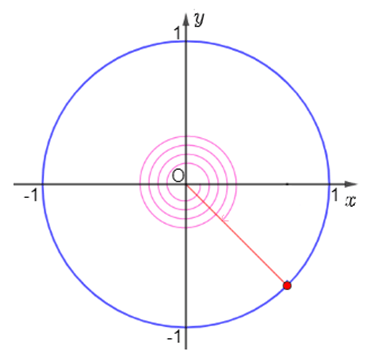
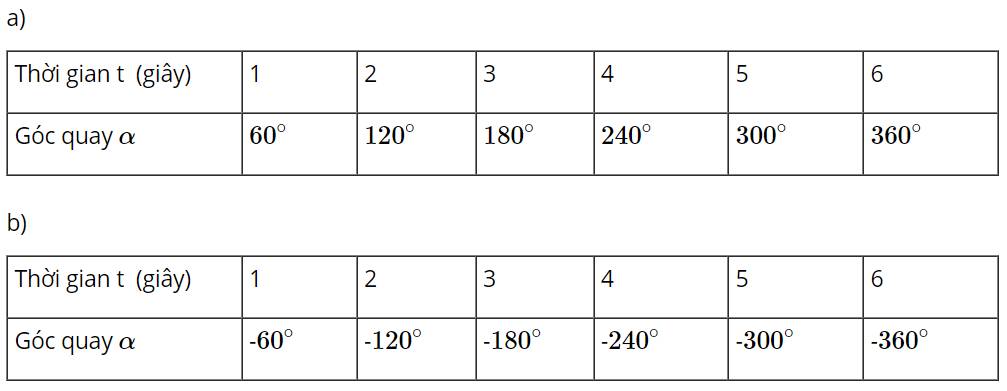
a) Khi quay bánh lái ngược chiều kim đồng hồ ( Hình 1), cứ mỗi giây, bánh lái quay một góc \( {60^0}\). Bảng dưới đây cho ta góc quay \(\alpha \)của thanh OM sau t giây kể từ lúc bắt đầu quay. Thay dấu ? bằng số đo thích hơp.

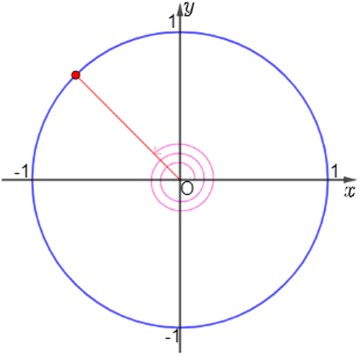
b) Nếu bánh lái được quay theo chiều ngược lại, nghĩa là quay cùng chiều kim đồng hồ ( Hình 2) với cùng tốc độ như trên, người ta ghi -\({60^ \circ }\)để chỉ góc mà thanh OM quay được sau mỗi giây. Bảng dưới đây cho ta góc quay \(\alpha \)của thanh OM sau t giây kể từ lúc bắt đầu quay. Thay dấu ? bằng số đo thích hợp.



Trả lời bởi Hà Quang Minh