Cho tam giác ABC. Chứng minh: \(A{B^2} + \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CA} = 0\)
$6. Tích vô hướng của hai vectơ
QL
Hướng dẫn giải
Thảo luận (1)
QL
Cho tam giác nhọn ABC, kẻ đường cao AH. Chứng minh rằng:
a) \(\overrightarrow {AB} .\overrightarrow {AH} = \overrightarrow {AC} .\overrightarrow {AH} \)
b) \(\overrightarrow {AB} .\overrightarrow {BC} = \overrightarrow {HB} .\overrightarrow {BC} \)
Hướng dẫn giải
Thảo luận (1)
Ta có: \(AH \bot CB \Rightarrow (\overrightarrow {AH} ,\overrightarrow {CB} ) = {90^o} \Leftrightarrow \cos (\overrightarrow {AH} ,\overrightarrow {CB} ) = 0 \Leftrightarrow \overrightarrow {AH} .\overrightarrow {CB} = 0\)
a) \(\overrightarrow {AB} .\overrightarrow {AH} - \overrightarrow {AC} .\overrightarrow {AH} = (\overrightarrow {AB} - \overrightarrow {AC} ).\overrightarrow {AH} = \overrightarrow {CB} .\overrightarrow {AH} = 0\)
\( \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AH} = \overrightarrow {AC} .\overrightarrow {AH} \)
b) \(\overrightarrow {AB} .\overrightarrow {BC} - \overrightarrow {HB} .\overrightarrow {BC} = (\overrightarrow {AB} - \overrightarrow {HB} ).\overrightarrow {BC} = (\overrightarrow {AB} + \overrightarrow {BH} ).\overrightarrow {BC} = \overrightarrow {AH} .\overrightarrow {BC} = 0\)
\( \Leftrightarrow \overrightarrow {AB} .\overrightarrow {BC} = \overrightarrow {HB} .\overrightarrow {BC} \)
Trả lời bởi Hà Quang Minh
QL
Nếu hai điểm M, N thỏa mãn \(\overrightarrow {MN} .\overrightarrow {NM} = - 4\) thì độ dài đoạn thẳng MN bằng bao nhiêu?
A. MN = 4
B. MN = 2
C. MN = 16
D. MN = 256
Hướng dẫn giải
Thảo luận (1)
\(\overrightarrow {MN} .\overrightarrow {NM} = \left| {\overrightarrow {MN} } \right|.\left| {\overrightarrow {NM} } \right|.\cos (\overrightarrow {MN} ,\overrightarrow {NM} ) = M{N^2}.\cos {180^o} = - M{N^2}\)
Do đó: \( - M{N^2} = - 4 \Leftrightarrow MN = 2.\)
Trả lời bởi Hà Quang Minh
QL
Cho hình vuông ABCD cạnh a. Tính các tích vô hướng sau:
a) \(\overrightarrow {AB} .\overrightarrow {AC} \)
b) \(\overrightarrow {AC} .\overrightarrow {BD} \)
Hướng dẫn giải
Thảo luận (1)
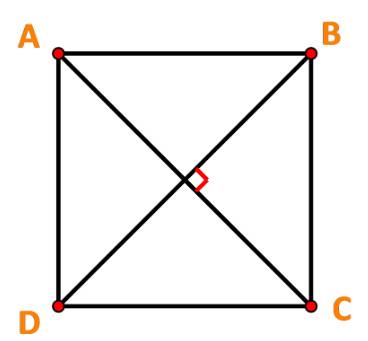
a) Ta có: \(AC = \sqrt {A{B^2} + A{D^2}} = \sqrt {2{a^2}} = a\sqrt 2 \)
\( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = a.a\sqrt 2 .\cos \widehat {BAC} = {a^2}\sqrt 2 \cos {45^o} = {a^2}.\)
b) Dễ thấy: \(AC \bot BD \Rightarrow (\overrightarrow {AC} ,\overrightarrow {BD} ) = {90^o}\)
\( \Rightarrow \overrightarrow {AC} .\overrightarrow {BD} = AC.BD.\cos {90^o} = AC.BD.0 = 0.\)
Trả lời bởi Hà Quang Minh
QL
Phát biểu nào sau đây là đúng?A. Nếu overrightarrow a ,overrightarrow b khác overrightarrow 0 và (overrightarrow a ,overrightarrow b ) {90^o} thì overrightarrow a .overrightarrow b 0B. Nếu overrightarrow a ,overrightarrow b khác overrightarrow 0 và (overrightarrow a ,overrightarrow b ) {90^o} thì overrightarrow a .overrightarrow b 0C. Nếu overrightarrow a ,overrightarrow b khác overrightarrow 0 và (overrightarrow a ,overrightarrow b ) {90^o} thì overrightarrow a .overrightarrow b ...
Đọc tiếp
Phát biểu nào sau đây là đúng?
A. Nếu \(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \) và \((\overrightarrow a ,\overrightarrow b ) < {90^o}\) thì \(\overrightarrow a .\overrightarrow b < 0\)
B. Nếu \(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \) và \((\overrightarrow a ,\overrightarrow b ) > {90^o}\) thì \(\overrightarrow a .\overrightarrow b > 0\)
C. Nếu \(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \) và \((\overrightarrow a ,\overrightarrow b ) < {90^o}\) thì \(\overrightarrow a .\overrightarrow b > 0\)
D. Nếu \(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \) và \((\overrightarrow a ,\overrightarrow b ) \ne {90^o}\) thì \(\overrightarrow a .\overrightarrow b < 0\)
Hướng dẫn giải
Thảo luận (1)
Ta có: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos (\overrightarrow a ,\overrightarrow b )\)
+) \((\overrightarrow a ,\overrightarrow b ) < {90^o} \Rightarrow \cos (\overrightarrow a ,\overrightarrow b ) > 0 \Leftrightarrow \overrightarrow a .\overrightarrow b > 0\)
Vậy A sai, C đúng, D sai.
+) \((\overrightarrow a ,\overrightarrow b ) > {90^o} \Rightarrow \cos (\overrightarrow a ,\overrightarrow b ) < 0 \Leftrightarrow \overrightarrow a .\overrightarrow b < 0\)
Vậy B sai.
Chọn C.
Trả lời bởi Hà Quang Minh
QL
Sử dụng tích vô hướng, chứng minh định lí Pythagore: Tam giác ABC vuông tại A khi và chỉ khi \(B{C^2} = A{B^2} + A{C^2}\).
Hướng dẫn giải
Thảo luận (1)
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\)
Ta có: \(\widehat A = {90^o}\) (tam giác ABC vuông tại A) \( \Leftrightarrow \cos A = \cos {90^o} = 0\)
\( \Leftrightarrow B{C^2} = A{B^2} + A{C^2}\) (đpcm)
Trả lời bởi Hà Quang Minh
QL
Cho tam giác ABC đều cạnh a, AH là đường cao. Tính:
a) \(\overrightarrow {CB} .\overrightarrow {BA} \)
b) \(\overrightarrow {AH} .\overrightarrow {BC} \)
Hướng dẫn giải
Thảo luận (1)
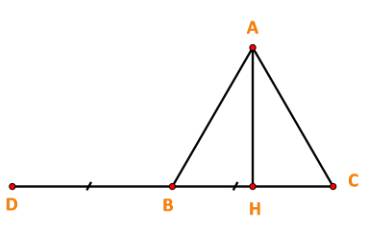
a) Vẽ vecto \(\overrightarrow {BD} = \overrightarrow {CB} \). Ta có:
\((\overrightarrow {CB} ,\overrightarrow {BA} ) = (\overrightarrow {BD} ,\overrightarrow {BA} ) = \widehat {DBA} = {120^o}\)
Vậy \(\overrightarrow {CB} .\overrightarrow {BA} = \left| {\overrightarrow {CB} } \right|.\left| {\overrightarrow {BA} } \right|\cos (\overrightarrow {CB} ,\overrightarrow {BA} ) = a.a.\cos {120^o} = {a^2}.\left( { - \frac{1}{2}} \right) = - \frac{{{a^2}}}{2}.\)
b) Vì \(AH \bot BC\) nên \[(\overrightarrow {AH} ,\overrightarrow {BC} ) = {90^o}\], suy ra \(\cos (\overrightarrow {AH} ,\overrightarrow {BC} ) = \cos {90^o} = 0.\)
Vậy \(\overrightarrow {AH} .\overrightarrow {BC} = \left| {\overrightarrow {AH} } \right|.\left| {\overrightarrow {BC} } \right|.\cos (\overrightarrow {AH} ,\overrightarrow {BC} ) = 0.\)
Trả lời bởi Hà Quang Minh
QL
Cho tam giác ABC vuông tại A có \(\widehat B = {30^o},AB = 3\;cm.\) Tính \(\overrightarrow {BA} .\overrightarrow {BC} ;\;\overrightarrow {CA} .\overrightarrow {CB} .\)
Hướng dẫn giải
Thảo luận (1)
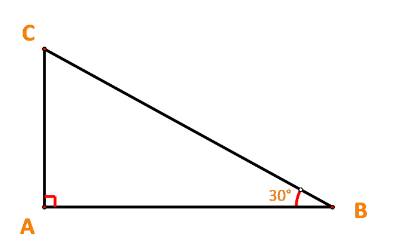
Ta có: \(BC = \frac{{AB}}{{\cos {{30}^o}}} = 3:\frac{{\sqrt 3 }}{2} = 2\sqrt 3 \); \(AC = BC.\sin \widehat {ABC} = 2\sqrt 3 .\sin {30^o} = \sqrt 3 .\)
\(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|\cos (\overrightarrow {BA} ,\overrightarrow {BC} ) = 3.2\sqrt 3 .\cos \widehat {ABC} = 6\sqrt 3 .\cos {30^o} = 6\sqrt 3 .\frac{{\sqrt 3 }}{2} = 9.\)
\(\overrightarrow {CA} .\overrightarrow {CB} = \left| {\overrightarrow {CA} } \right|.\left| {\overrightarrow {CB} } \right|\cos (\overrightarrow {CA} ,\overrightarrow {CB} ) = \sqrt 3 .2\sqrt 3 .\cos \widehat {ACB} = 6.\cos {60^o} = 6.\frac{1}{2} = 3.\)
Trả lời bởi Hà Quang Minh
QL
Chứng minh rằng với hai vecto bất kì overrightarrow a ,overrightarrow b , ta có:begin{array}{l}{(overrightarrow a + overrightarrow b )^2} {overrightarrow a ^2} + 2overrightarrow a .overrightarrow b + {overrightarrow b ^2}{(overrightarrow a - overrightarrow b )^2} {overrightarrow a ^2} - 2overrightarrow a .overrightarrow b + {overrightarrow b ^2}overrightarrow a - overrightarrow b )(overrightarrow a + overrightarrow b ) {overrightarrow a ^2} - {overrightarrow b ^2}end{array}
Đọc tiếp
Chứng minh rằng với hai vecto bất kì \(\overrightarrow a ,\overrightarrow b \), ta có:
\(\begin{array}{l}{(\overrightarrow a + \overrightarrow b )^2} = {\overrightarrow a ^2} + 2\overrightarrow a .\overrightarrow b + {\overrightarrow b ^2}\\{(\overrightarrow a - \overrightarrow b )^2} = {\overrightarrow a ^2} - 2\overrightarrow a .\overrightarrow b + {\overrightarrow b ^2}\\(\overrightarrow a - \overrightarrow b )(\overrightarrow a + \overrightarrow b ) = {\overrightarrow a ^2} - {\overrightarrow b ^2}\end{array}\)
Hướng dẫn giải
Thảo luận (1)
\(\begin{array}{l}{ + \, (\overrightarrow a + \overrightarrow b )^2} = (\overrightarrow a + \overrightarrow b )(\overrightarrow a + \overrightarrow b )\\ = \overrightarrow a .(\overrightarrow a + \overrightarrow b ) + \overrightarrow b .(\overrightarrow a + \overrightarrow b ) \\= {\overrightarrow a ^2} + \overrightarrow a .\overrightarrow b + \overrightarrow b .\overrightarrow a + {\overrightarrow b ^2} \\= {\overrightarrow a ^2} + 2\overrightarrow a .\overrightarrow b + {\overrightarrow b ^2}.\\ + \, {(\overrightarrow a - \overrightarrow b )^2} =(\overrightarrow a - \overrightarrow b )(\overrightarrow a - \overrightarrow b )\\ = \overrightarrow a .(\overrightarrow a - \overrightarrow b ) - \overrightarrow b .(\overrightarrow a - \overrightarrow b ) \\= {\overrightarrow a ^2} - \overrightarrow a .\overrightarrow b - \overrightarrow b .\overrightarrow a + {\overrightarrow b ^2} \\= {\overrightarrow a ^2} - 2\overrightarrow a .\overrightarrow b + {\overrightarrow b ^2}. \\ + \, (\overrightarrow a - \overrightarrow b )(\overrightarrow a + \overrightarrow b ) \\= \overrightarrow a .(\overrightarrow a - \overrightarrow b ) + \overrightarrow b .(\overrightarrow a - \overrightarrow b ) \\= {\overrightarrow a ^2} - \overrightarrow a .\overrightarrow b + \overrightarrow b .\overrightarrow a - {\overrightarrow b ^2} \\= {\overrightarrow a ^2} - {\overrightarrow b ^2}.\end{array}\)
Trả lời bởi Hà Quang Minh
QL
Tính overrightarrow a .overrightarrow b trong mỗi trường hợp sau:a) left| {overrightarrow a } right| 3,;left| {overrightarrow b } right| 4,;(overrightarrow a ,overrightarrow b ) {30^o}b) left| {overrightarrow a } right| 5,;left| {overrightarrow b } right| 6,;(overrightarrow a ,overrightarrow b ) {120^o}c) left| {overrightarrow a } right| 2,;left| {overrightarrow b } right| 3,;overrightarrow a và overrightarrow b cùng hướng.d) left| {overrightarrow a } right| 2,;left| {overrightarrow...
Đọc tiếp
Tính \(\overrightarrow a .\overrightarrow b \) trong mỗi trường hợp sau:
a) \(\left| {\overrightarrow a } \right| = 3,\;\left| {\overrightarrow b } \right| = 4,\;(\overrightarrow a ,\overrightarrow b ) = {30^o}\)
b) \(\left| {\overrightarrow a } \right| = 5,\;\left| {\overrightarrow b } \right| = 6,\;(\overrightarrow a ,\overrightarrow b ) = {120^o}\)
c) \(\left| {\overrightarrow a } \right| = 2,\;\left| {\overrightarrow b } \right| = 3,\;\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
d) \(\left| {\overrightarrow a } \right| = 2,\;\left| {\overrightarrow b } \right| = 3,\;\overrightarrow a \) và \(\overrightarrow b \) ngược hướng
Hướng dẫn giải
Thảo luận (1)
a) \(\overrightarrow a .\overrightarrow b = 3.4.\cos {30^o} = 12.\frac{{\sqrt 3 }}{2} = 6\sqrt 3 \)
b) \(\overrightarrow a .\overrightarrow b = 5.6.\cos {120^o} = 30.\left( { - \frac{1}{2}} \right) = - 15\)
c) \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng nên \((\overrightarrow a ,\overrightarrow b ) = {0^o}\)
\(\overrightarrow a .\overrightarrow b = 2.3.\cos {0^o} = 6.1 = 6\)
d) \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng nên \((\overrightarrow a ,\overrightarrow b ) = {180^o}\)
\(\overrightarrow a .\overrightarrow b = 2.3.\cos {180^o} = 6.( - 1) = - 6\)
Trả lời bởi Hà Quang Minh
\(\begin{array}{l}A{B^2} + \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CA} = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CA} \\ = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} ) = \overrightarrow {AB} (\overrightarrow {AC} + \overrightarrow {CA} ) = \overrightarrow {AB} .\overrightarrow 0 = 0.\end{array}\)
Trả lời bởi Hà Quang Minh