Tính phương sai và độ lệch chuẩn của bản phân bố tần số đã được lập ở bài 1 và của bảng phân bố tần số ghép lớp


Tính phương sai và độ lệch chuẩn của bản phân bố tần số đã được lập ở bài 1 và của bảng phân bố tần số ghép lớp


Hai lớp 10C và 10D một trường trung học phổ thông đồng thời làm bài thi môn ngữ văn theo cùng một đề thi. Kết quả thi được trình bày ở hai bảng phân bố tần số sau đây :

a. Tính các số trung bình cộng, phương sai, độ lệch chuẩn của các bảng phân bố tần số đã cho ?
b. Xét xem kết quả làm bài thi của môn Ngữ văn ở lớp nào đồng đều hơn ?
a) Số trung bình điểm thi Ngữ văn của lớp 10C và 10D tương ứng là
.(3x5 + 7x6 + 12x7 + 14x8 + 3x9 + 1x10) = 7,25
.(8x6+18x7+10x8+4x9) = 7,25.
Phương sai bảng điểm thi Văn của hai lớp theo thứ tự là:
= 1,2875
= 0,7875.
Độ lệch chuẩn theo thứ tự là Sx ≈ 1,1347 Sy ≈ 0,8874.
b) Qua xem xét các số đặc trung ta thấy điểm trung bình thi văn 2 lớp 10C và 10D là như nhau (đều bằng 7,25). Nhưng phương sai của bảng điểm thi lớp 10D nhỏ hơn phương sai tương ứng ở lớp 10C. Điều đó chứng tỏ kết quả làm bài thi Văn ở lớp 10D đồng đều hơn.
Cho hai bảng phân bố tần số ghép lớp :

a. Tính các số trung bình cộng của các bảng phân bố tần số ghép lớp đã cho ?
b. Tính phương sai của các bảng phân bố tần số ghép lớp đã cho ?
c. Xem xét nhóm cá nào có khối lượng đồng đều hơn ?
a), b) Số trung bình cộng của nhóm cá thứ nhất:
.(4x0,7 + 6x0,9 + 6x1.1 + 4x1,3) = 1
Phương sai: .(4x0,72 + 6x0,92 + 6x1,12 + 4x1,32) – 1 = 0,042
Độ lệch chuẩn: Sx = 0,2
Đối với nhóm cá thứ hai:
Số trung bình: .(3x0,6 + 4x0,8 + 6x1 + 4x1,2 + 3x1,4) = 1
Phương sai: .(3x0,62 + 4x0,82 + 6x12 + 4x1,22 + 3x1,42) – 1 = 0,064
Độ lệch chuẩn: Sx = ≈ 0,25.
c) Ta thấy = 1, trọng lượng trung bình hai nhóm cá bằng nhau nhưng
<
chứng tỏ mức độ phân tán các giá trị so với giá trị trung bình của nhóm cá thứ hai lớn hơn. Nghĩa là khối lượng nhóm cá thứ nhất đồng đều hơn nhóm cá thứ hai.
a) Tính phương sai và độ lệch chuẩn của dãy số liệu về chiều cao của các học sinh nam và các học sinh nữ ở bảng 5 ?
Chiều cao của 120 học sinh lớp 11 ở trường Trung học phổ thông M (đơn vị : cm)
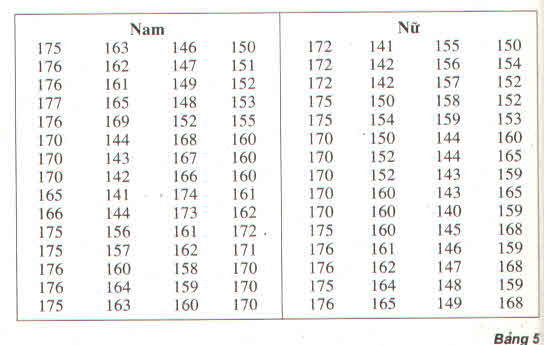
b) Giả sử trường Trung học phổ thông M còn có một nhóm học sinh nam lớp 10 chuyên toán (kí hiệu là nhóm T) có chiều cao trung binh là \(\overline{x}=163cm\), có độ lệch chuẩn là \(s=13\) . So sánh chiều cao của 3 nhóm học sinh đã cho (nhóm nam, nhóm nữ, nhóm T)
a) Dãy các số liệu chiều cao của các học sinh nam ở bảng 5 có :
\(\overline{x_1}\approx163\left(cm\right);s_1^2\approx134,3;s_1\approx11,59\)
Dãy các số liệu chiều cao của các học sinh nữ cho ở bảng 5 có :
\(\overline{x_2}\approx159,5\left(cm\right);s_2^2\approx148;s_2\approx12,17\)
b) Nhóm T có \(\overline{x_3}=163\left(cm\right);s_3^2=169;s_3=13\)
Học sinh ở nhóm nam và nhóm T có chiều cao như nhau và cùng lớn hơn chiều cao của học sinh ở nhóm nữ (vì \(\overline{x}_1=\overline{x}_3>\overline{x}_2\)
Vì \(\overline{x}_1=\overline{x}_3=163\left(cm\right)\) và \(s_1< s_3\) nên chiều cao của các học sinh nam đồng đều hơn chiều cao của các học sinh nhóm T
Trả lời bởi Nguyen Thuy HoaHai xạ thủ cùng tập bắn, mỗi người đã bắn 30 viên đạn vào bia. Kết quả được ghi lại ở các bảng sau :
Điểm số của xạ thủ A

Điểm số của xạ thủ B

a) Tính số trung bình, phương sai và độ lệch chuẩn của các số liệu thống kê cho ở bảng 13, bảng 14
b) Xem xét trong lần tập bắn này, xạ thủ nào bắn chụm hơn ?
a) Điểm số của xạ thủ A có : \(\overline{x}\approx8,3\) điểm ; \(s_1^2\approx1,6;s_1\approx1,27\) điểm
Điểm số của xạ thủ B có \(\overline{y}=8,4\) điểm, \(s_2^2\approx1,77;s_2\approx1,33\) điểm
b) \(\overline{x}\approx\overline{y}=8,4\) điểm; \(s_1^2< s_2^2\), như vậy mức độ phân tán của các điểm số (so với số trung bình) của xạ thủ A là bé hơn. Vì vậy trong lần tập bắn này xạ thủ A bắn chụm hơn.
Trả lời bởi Nguyen Thuy HoaNgười ta điều tra sản phẩm của hai tổ đóng gói các túi đường (có khối lượng quy định là 2kg). Kết quả điều tra cho các số liệu thống kê ghi ở hai bảng sau :

a) Lập bảng phân bố tần số và tần suất ghép lớp theo sản phẩm của tổ A với các lớp
[1,90; 1,98); [1,98; 2,06); [2,06; 2,14); [2,14; 2,22); [2,22; 2,30]
b) Lập bảng phân bố tần số và tần suất ghép lớp theo sản phẩm của tổ B vói các lớp
[1,5; 1,7); [1,7; 1,9); [1,9; 2,1); [2,1; 2,3); [2,3; 2,30]
c) Tính số trung bình, phương sai và độ lệch chuẩn của các số liệu thống kê cho ở bảng 15, bảng 16. Từ đó, xét xem trong lần điều tra này, sản phẩm của tổ nào có khối lượng đồng đều hơn ?
a) Phương sai và độ lệch chuẩn trong bài tập 1. Bảng phân bố tần số viết lại là
Số trung bình: \(\overline{x} = 1170\)
Phương sai: \(S_{x}^{2}=\frac{1}{30}(3x1150^{2}+6x1160^{2}+12x1170^{2}+6x1180^{2}+3x1190^{2})-1170^{2} = 120\)
Độ lệch chuẩn: Sx.= \(\sqrt{S_{x}^{2}}=\sqrt{120} ≈ 10,9545\)
b) Phương sai và độ lệch chuẩn, bảng thống kê trong bài tập 2 \(\S 1.\)
\(S_{x}^{2}=\frac{1}{60}(8x15^{2}+18x25^{2}+24x35^{2}+10x45^{2}) - 312 = 84 \)
Sx ≈ 9,165.
Trả lời bởi qwerty