Một chiếc ăng - ten chảo parabol có chiều cao h = 0,5 m và đường kính d = 4m. Ở mặt cắt qua trục ta được một parabol dạng \(y=ax^2\) (h.24)
Hãy xác định hệ số a ?
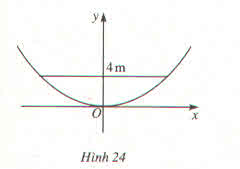
Một chiếc ăng - ten chảo parabol có chiều cao h = 0,5 m và đường kính d = 4m. Ở mặt cắt qua trục ta được một parabol dạng \(y=ax^2\) (h.24)
Hãy xác định hệ số a ?

Một chiếc cổng hình parabl dạng \(y=-\dfrac{1}{2}x^2\) có chiều rộng \(d=8m\). Hãy tính chiều cao h của cổng (h.25) ?
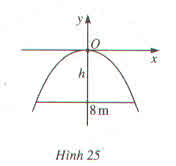
Lời giải
Parabol nhận trục tung là trục đối xứng
(điểm thấp nhất thuộc đồ thị có tọa độ A(4,ya)
\(y\left(4\right)=-\dfrac{1}{2}.4^2=-8\)
Vậy chiều cao cổng là 8m
Trả lời bởi ngonhuminh
Xác định trục đối xứng, tọa độ đỉnh, các giao điểm với trục tung và trục hoành của parabol ?
a) \(y=2x^2-x-2\)
b) \(y=-2x^2-x+2\)
c) \(y=-\dfrac{1}{2}x^2+2x-1\)
d) \(y=\dfrac{1}{5}x^2-2x+6\)
Lời giải
a)
a.1) Trục đối xứng y =1/4
a.2) giao trục tung A(0,-2)
a.3) giao trục hoành (\(\left(\Delta=17\right)\) \(B\left(\dfrac{1-\sqrt{17}}{4};0\right)\);\(C\left(\dfrac{1+\sqrt{17}}{4}\right)\)
b)
b.1) Trục đối xứng y =-1/4
b.2) giao trục tung A(0,2)
a.3) giao trục hoành \(\left(\Delta=17\right)\) \(B\left(\dfrac{-1-\sqrt{17}}{4};0\right)\);\(C\left(\dfrac{-1+\sqrt{17}}{4}\right)\)
Trả lời bởi ngonhuminh
Viết phương trình của parabol \(y=ax^2+bx+c\) ứng với mỗi đồ thị dưới đây ?
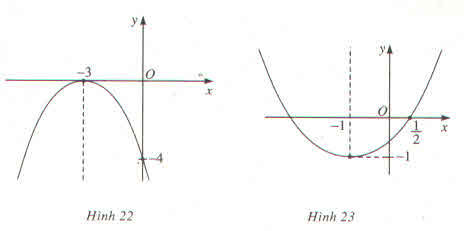
Hình 22
y=ax^2 +bx+c thỏa mãn hệ
\(\left\{{}\begin{matrix}y\left(0\right)=-4\Rightarrow c=-4\\y\left(-3\right)=9a-3b-4=0\\y\left(-6\right)=36a-6b-4=-4\end{matrix}\right.\)
(3) -(2) nhân 2
\(36a-18a-4+8=-4\Rightarrow18a=-8\Rightarrow a=\dfrac{-8}{18}=\dfrac{-4}{9}\)
Thế vào (2) -4-3b-4=0 => b=-8/3
Vậy pa ra bo; cho hình 22 là
\(y=-\dfrac{4}{9}x^2-\dfrac{8}{3}x-4\)
Trả lời bởi ngonhuminh
Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai :
a) \(y=2x^2+4x-6\)
b) \(y=-3x^2-6x+4\)
c) \(y=\sqrt{3}x^2+2\sqrt{3}x+2\)
d) \(y=-2\left(x^2+1\right)\)
Xác định a, b, c biết parabol \(y=ax^2+bx+c\) đi qua điểm \(A\left(8;0\right)\) và có đỉnh là \(I\left(6;-12\right)\)
Hàm số đi qua \(A\left(8;0\right)\) nên: \(a.8^2+8b+c=0\)\(\Leftrightarrow64a+8b+c=0\).
Hàm số có đỉnh là: \(I\left(6;-12\right)\) nên: \(\left\{{}\begin{matrix}\dfrac{-b}{2a}=6\\6^2.a+6b+c=-12\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}12a+b=0\\36a+6b+c=-12\end{matrix}\right.\).
Vậy ta có hệ: \(\left\{{}\begin{matrix}64a+8b+c=0\\-b=12a\\36a+6b+c=-12\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=-36\\c=96\end{matrix}\right.\).
Vậy : \(y=-3x^2-36x+96\).
Lập bảng biến thiên và vẽ đồ thị của các hàm số :
a. \(y=3x^2-4x+1\)
b. \(y=-3x^2+2x-1\)
c. \(y=4x^2-4x+1\)
d. \(y=-x^2+4x-4\)
e. \(y=2x^2+x+1\)
f. \(y=-x^2+x-1\)
a) Bảng biến thiên:
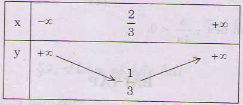
Đồ thị: - Đỉnh: 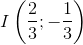
- Trục đối xứng: 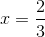
- Giao điểm với trục tung A(0; 1)
- Giao điểm với trục hoành 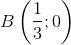 , C(1; 0).
, C(1; 0).
(hình dưới).
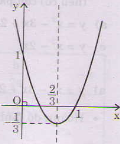
b) y = - 3x2 + 2x – 1= 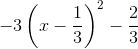
Bảng biến thiên:
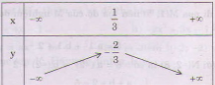
Vẽ đồ thị: - Đỉnh 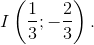 Trục đối xứng:
Trục đối xứng: 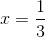 .
.
- Giao điểm với trục tung A(0;- 1).
- Giao điểm với trục hoành: không có.
Ta xác định thêm mấy điểm: B(1;- 2), C(1;- 6). (bạn tự vẽ).
c) y = 4x2 - 4x + 1 = 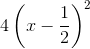 .
.
Lập bảng biến thiên và vẽ tương tự câu a, b.
d) y = - x2 + 4x – 4 = - (x – 2)2
Bảng biến thiên:
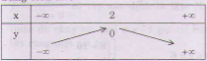
Cách vẽ đồ thị:
Ngoài cách vẽ như câu a, b, ta có thể vẽ như sau:
+ Vẽ đồ thị (P) của hàm số y = - x2.
+ Tịnh tiến (P) song song với Ox sang phải 2 đơn vị được (P1) là đồ thị cần vẽ. (hình dưới).
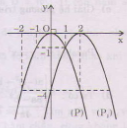
e) y = 2x2+ x + 1;
- Đỉnh I \(\left(\dfrac{-1}{4};\dfrac{-7}{8}\right)\)
- Trục đối xứng :\(x=\dfrac{-1}{4}\)
- Giao Ox: Đồ thị không giao với trục hoành
- Giao Oy: Giao với trục tung tại điểm (0;1)
Bảng biến thiên:
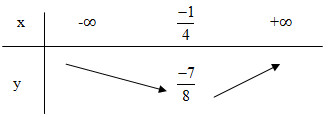
Vẽ đồ thị theo bảng sau:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 7 | 2 | 1 | 4 | 11 |
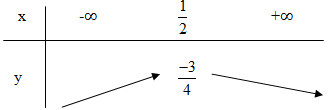
f) y = - x2 + x - 1.
- Đỉnh I \(\left(\dfrac{1}{2};\dfrac{-3}{4}\right)\)
- Trục đối xứng : \(x=\dfrac{1}{2}\)
- Giao Ox: Đồ thị không giao với trục hoành
- Giao Oy: Giao với trục tung tại điểm (0;-1)
Bảng biến thiên:
Vẽ đồ thị theo bảng sau:
| x | -2 | -1 | 0 | 1 | 2 |
| y | -7 | -3 | -1 | -1 | -3 |
Trả lời bởi Hai Binh
Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của mỗi parabol :
a. \(y=x^2-3x+2\)
b. \(y=-2x^2+4x-3\)
c. \(y=x^2-2x\)
d. \(y=-x^2+4\)
a) y = x2 - 3x + 2. Hệ số: a = 1, b = - 3, c = 2.
Hoành độ đỉnh x1 = Vậy đỉnh parabol là .
x2 - 3x + 2 = 0 ⇔ x1 = , x1 =
.
Vậy các giao điểm của parabol với trục hoành là B(1; 0) và C(2; 0).
b) Đỉnh I(1; 1). Giao điểm với trục tung A(0;- 3).
Phương trình - 2x2 + 4x - 3 = 0 vô nghiệm. Không có giao điểm cuả parabol với trục hoành.
c) Đỉnh I(1;- 1). Các giao điểm với hai trục tọa độ: A(0; 0), B(2; 0).
d) Đỉnh I(0; 4). Các giao điểm với hai trục tọa độ: A(0; 4), B(- 2; 0), C(2; 0).
Trả lời bởi Hai Binh
Xác định parabol \(y=ax^2+bx+2\), biết rằng parabol đó :
a. Đi qua hai điểm \(M\left(1;5\right)\) và \(N\left(-2;8\right)\)
b. Đi qua điểm \(A\left(3;-4\right)\) và có trục đối xứng là \(x=-\dfrac{3}{2}\)
c. Có đỉnh là \(I\left(2;-2\right)\)
d. Đi qua điểm \(B\left(-1;6\right)\) và tung độ của đỉnh là \(-\dfrac{1}{4}\)
a) Vì parabol đi qua M(1; 5) nên tọa độ của M nghiệm đúng phương trình của parabol: 5 = a.12 + b.1 + 2.
Tương tự, với N(- 2; 8) ta có: 8 = a.(- 2)2 + b.(- 2) + 2
Giải hệ phương trình: ta được a = 2, b = 1.
Parabol có phương trình là: y = 2x2 + x + 2.
b) Giải hệ phương trình:
Parabol: y = x2 - x + 2.
c) Giải hệ phương trình:
Parabol: y = x2 - 4x + 2.
d) Ta có:
Parabol: y = 16x2 + 12x + 2 hoặc y = x2 - 3x + 2.
Xác định hàm số bậc hai \(y=ax^2-4x+c\), biết rằng đồ thị của nó
a) Đi qua hai điểm \(A\left(1;-2\right);B\left(2;3\right)\)
b) Có đỉnh là \(I\left(-2;-1\right)\)
c) Có hoành độ đỉnh là -3 và đi qua điểm \(P\left(-2;1\right)\)
d) Có trục đối xứng là đường thẳng \(x=2\) và cắt trục hoành tại điểm \(M\left(3;0\right)\)
a)
y(1) =a-4+c=\(-2\)\(\Rightarrow\) a+c=2
y(2)=4a-8+c=3 \(\Rightarrow\)4a+c=3
Trừ cho nhau\(\Rightarrow\)3a=1 \(\Rightarrow\)a=\(\dfrac{1}{3}\)\(\Rightarrow\) \(c=2-\dfrac{1}{3}=\dfrac{5}{3}\).
Vậy: \(y=\dfrac{1}{3}x^2-4x+\dfrac{5}{3}\).
b)
I(-2;1)\(\Rightarrow\dfrac{4}{2a}=-2\)\(\Leftrightarrow a=-1\).
y(-2) \(=-4+8+c=1\)\(\Rightarrow\) \(c=-3\)
Vậy: \(y=-x^2-4x-3\).
c)\(\dfrac{4}{2a}=-3\)\(\Leftrightarrow a=-\dfrac{2}{3}\)
\(y\left(-2\right)=-\dfrac{2}{3}.4+8+c=1\)\(\Leftrightarrow c=-\dfrac{13}{3}\)
Vậy: \(y=-\dfrac{2}{3}x^3-4x-\dfrac{13}{3}\).
Pra bol đối xứng qua trục Tung => điểm cao nhất thuộc Parabol có tọa độ (2,h)
\(x=2\Rightarrow y=\dfrac{1}{2}\Rightarrow a.2^2=\dfrac{1}{2}\Rightarrow a=\dfrac{1}{8}\)
Trả lời bởi ngonhuminh