Cho đoạn thẳng AB và điểm M nằm giữa A và B sao cho \(AM>MB\). Vẽ các vectơ \(\overrightarrow{MA}+\overrightarrow{MB}\) và \(\overrightarrow{MA}-\overrightarrow{MB}\) ?
§2. Tổng và hiệu của hai vectơ
SK
Hướng dẫn giải
Thảo luận (1)
SK
Cho hình bình hành ABCD và một điểm M tùy ý. Chứng minh rằng \(\overrightarrow{MA+}\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\) ?
Hướng dẫn giải
Thảo luận (1)
SK
Chứng minh rằng đối với tứ giác ABCD bất kì ta luôn có :
a) \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{O}\)
b) \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{CB}-\overrightarrow{CD}\)
Hướng dẫn giải
Thảo luận (1)
SK
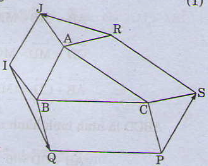
Cho tam giác ABC. Bên ngoài của tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng \(\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{O}\) ?
Hướng dẫn giải
Thảo luận (1)
Ta xét tổng:
+
+
+
+
+
=
=
(1)
Mặt khác, ta có ABIJ, BCPQ và CARS là các hình bình hành nên:
=
=
=
=> +
+
=
+
+
=
=
(2)
Từ (1) và (2) suy ra : +
+
=
(dpcm)
SK
Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ \(\overrightarrow{AB}+\overrightarrow{BC}\) và \(\overrightarrow{AB}-\overrightarrow{BC}\) ?
Hướng dẫn giải
Thảo luận (1)
SK
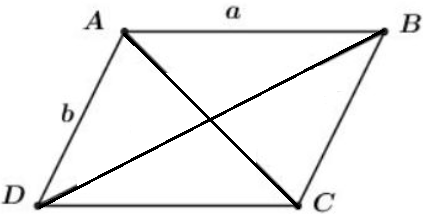
Cho hình bình hành ABCD có tâm O. Chứng minh rằng :
a) overrightarrow{CO}-overrightarrow{OB}overrightarrow{BA}
b) overrightarrow{AB}-overrightarrow{BC}overrightarrow{DB}
c) overrightarrow{DA}-overrightarrow{DB}overrightarrow{OD}-overrightarrow{OC}
d) overrightarrow{DA}-overrightarrow{DB}+overrightarrow{DC}overrightarrow{0}
Đọc tiếp
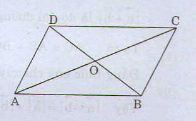
Cho hình bình hành ABCD có tâm O. Chứng minh rằng :
a) \(\overrightarrow{CO}-\overrightarrow{OB}=\overrightarrow{BA}\)
b) \(\overrightarrow{AB}-\overrightarrow{BC}=\overrightarrow{DB}\)
c) \(\overrightarrow{DA}-\overrightarrow{DB}=\overrightarrow{OD}-\overrightarrow{OC}\)
d) \(\overrightarrow{DA}-\overrightarrow{DB}+\overrightarrow{DC}=\overrightarrow{0}\)
Hướng dẫn giải
Thảo luận (1)
a) Ta có, theo quy tắc ba điểm của phép trừ:
=
-
(1)
Mặt khác, =
(2)
Từ (1) và (2) suy ra:
=
-
.
b) Ta có : =
-
(1)
=
(2)
Từ (1) và (2) cho ta:
=
-
.
c) Ta có :
-
=
(1)
-
=
(2)
=
(3)
Từ (1), (2), (3) suy ra đpcm.
d) -
+
= (
-
) +
=
+
=
+
( vì
=
) =
Trả lời bởi qwerty
SK
Cho \(\overrightarrow{a},\overrightarrow{b}\) là hai vectơ khác \(\overrightarrow{0}\). Khi nào có đẳng thức :
a) \(\left|\overrightarrow{a}+\overrightarrow{b}\right|=\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|\)
b) \(\left|\overrightarrow{a}+\overrightarrow{b}\right|=\left|\overrightarrow{a}-\overrightarrow{b}\right|\)
Hướng dẫn giải
Thảo luận (2)
SK
Cho \(\left|\overrightarrow{a}+\overrightarrow{b}\right|=0\). So sánh độ dài, phương và hướng của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) ?
Hướng dẫn giải
Thảo luận (1)
Từ = 0, ta có
+
= 0 =>
= -
Điều này chứng tỏ hai vectơ có cùng độ dài =
, cùng phương và ngược hướng
SK
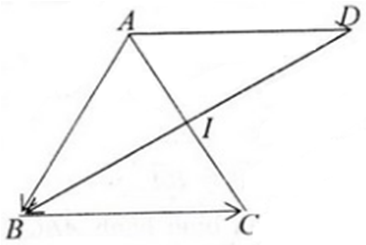
Chứng minh rằng \(\overrightarrow{AB}=\overrightarrow{CD}\) khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau ?
Hướng dẫn giải
Thảo luận (1)
Nếu \(\overrightarrow{AB}=\overrightarrow{CD}\) thì AD và BC có trung điểm trùng nhau. Gọi I là trung điểm của AD ta chứng minh I cũng là trung điểm của BC.
Theo quy tắc của ba điểm của tổng, ta có
\(\overrightarrow{AB}=\overrightarrow{AI}+\overrightarrow{IB};\overrightarrow{CD}=\overrightarrow{CI}+\overrightarrow{ID}\)
Vì \(\overrightarrow{AB}=\overrightarrow{CD}\) nên \(\overrightarrow{AI}+\overrightarrow{IB}=\overrightarrow{CI}+\overrightarrow{ID}\)
\(\Rightarrow\overrightarrow{AI}-\overrightarrow{ID}=\overrightarrow{CI}-\overrightarrow{IB}\)
\(\Rightarrow\overrightarrow{AI}+\overrightarrow{DI}=\overrightarrow{CI}+\overrightarrow{BI}\left(1\right)\)
Vì I là trung điểm của AD nên \(\overrightarrow{AI}+\overrightarrow{DI}=\overrightarrow{0}\left(2\right)\)
Từ (1) và (2) suy ra \(\overrightarrow{CI}+\overrightarrow{BI}=\overrightarrow{0}\left(3\right)\)
Từ (3) ta có chung điểm I, ta chứng minh \(\overrightarrow{AB}=\overrightarrow{CD}\)
I là trung điểm AD \(\Rightarrow\overrightarrow{AI}+\overrightarrow{DI}=\overrightarrow{0}\Rightarrow\overrightarrow{AI}-\overrightarrow{ID}=\overrightarrow{0}\)
I là trung điểm BC \(\Rightarrow\overrightarrow{CI}+\overrightarrow{BI}=0\Rightarrow\overrightarrow{CI}-\overrightarrow{IB}=\overrightarrow{0}\)
Suy ra \(\overrightarrow{AI}-\overrightarrow{ID}=\overrightarrow{CI}-\overrightarrow{IB}\)
\(\Rightarrow\overrightarrow{AI}+\overrightarrow{IB}=\overrightarrow{CI}+\overrightarrow{ID}\Rightarrow\overrightarrow{AB}=\overrightarrow{CD}\)
SK
Cho ba lực overrightarrow{F_1}overrightarrow{MA};overrightarrow{F_2}overrightarrow{MB};overrightarrow{F_3}overrightarrow{MC} cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của overrightarrow{F_1},overrightarrow{F_2} đều là 100N và widehat{AMB}60^0. Tìm cường độ và hướng của lực overrightarrow{F_3} ?
Đọc tiếp
Cho ba lực \(\overrightarrow{F_1}=\overrightarrow{MA};\overrightarrow{F_2}=\overrightarrow{MB};\overrightarrow{F_3}=\overrightarrow{MC}\) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow{F_1},\overrightarrow{F_2}\) đều là 100N và \(\widehat{AMB}=60^0\). Tìm cường độ và hướng của lực \(\overrightarrow{F_3}\) ?
Hướng dẫn giải
Thảo luận (1)
\(\left|\overrightarrow{F_3}\right|=100\sqrt{3}\) và \(\overrightarrow{F_3}\) ngược hướng với hướng \(\overrightarrow{ME}\) với E là đỉnh thứ tư của hình bình hành MACB
Trả lời bởi Truy kích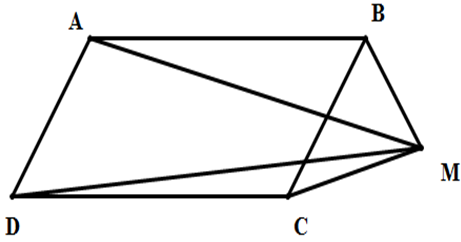
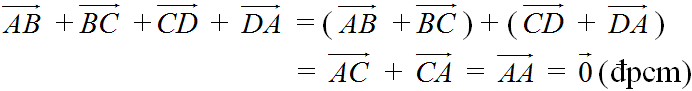

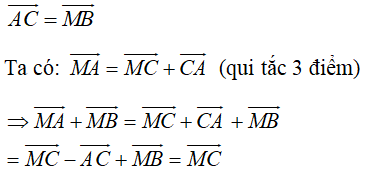
Trả lời bởi Quang Duy