Cho tứ giác ABCD, chứng minh rằng nếu : \(\overrightarrow{AB}=\overrightarrow{DC}\) thì \(\overrightarrow{AD}=\overrightarrow{BC}\) ?
§1. Các định nghĩa
SK
Hướng dẫn giải
Thảo luận (2)
SK
Xác định vị trí tương đối của ba điểm phân biệt A, B và C trong các trường hợp sau :
a) overrightarrow{AB} và overrightarrow{AC} cùng hướng, left|overrightarrow{AB}right|left|overrightarrow{AC}right|
b) overrightarrow{AB} và overrightarrow{AC} ngược hướng
c) overrightarrow{AB} và overrightarrow{AC} cùng phương
Đọc tiếp
Xác định vị trí tương đối của ba điểm phân biệt A, B và C trong các trường hợp sau :
a) \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) cùng hướng, \(\left|\overrightarrow{AB}\right|>\left|\overrightarrow{AC}\right|\)
b) \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) ngược hướng
c) \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) cùng phương
Hướng dẫn giải
Thảo luận (3)
a)
A, B, C thẳng hàng và C nằm giữa A và B.
SK
Hãy tính số các vectơ (khác \(\overrightarrow{0}\)) mà các điểm đầu và điểm cuối được lấy từ các điểm phân biệt đã cho trong các trường hợp sau :
a) Hai điểm
b) Ba điểm
c) Bốn điểm
Hướng dẫn giải
Thảo luận (1)
a) Có hai véc tơ.
b)
Số đoạn thẳng tạo thành từ 3 điểm A, B, C là:\(\dfrac{3.2}{2}=3\) đoạn.
Mỗi đoạn thẳng tạo thành hai véc tơ đối nhau nên số véc tơ là:
\(3.2=6\) (véc tơ).
b) Số đoạn thẳng tạo thành từ 4 điểm phân biệt là:
\(4.3:2=6\) (đoạn).
Số véc tơ tạo thành là:
6.2 = 12 (véc tơ).
SK
Cho tam giác ABC. Các điểm M và N lần lượt là trung điểm các cạnh AB và AC. So sánh độ dài của hai vectơ \(\overrightarrow{NM}\) và \(\overrightarrow{BC}\). Vì sao có thể nói hai vectơ này cùng phương ?
Hướng dẫn giải
Thảo luận (1)
Do M, N là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC nên MN//BC.
Do vậy hai véc tơ \(\overrightarrow{NM}\) và \(\overrightarrow{BC}\) cùng phương.
SK
Cho hình vuông ABCD tâm O. Liệt kê tất cả các vectơ bằng nhau (khác \(\overrightarrow{0}\)) nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối ?
Hướng dẫn giải
Thảo luận (1)
\(\overrightarrow{AO}=\overrightarrow{OC};\overrightarrow{DO}=\overrightarrow{OB}\);
\(\overrightarrow{OA}=\overrightarrow{CO};\overrightarrow{DO}=\overrightarrow{OB}\).
SK
Cho lục giác ABCDEF có tâm O
a) Tìm các vectơ khác \(\overrightarrow{0}\) và cùng phương với \(\overrightarrow{OA}\)
b) Tìm các vectơ bằng vectơ \(\overrightarrow{AB}\)
Hướng dẫn giải
Thảo luận (1)
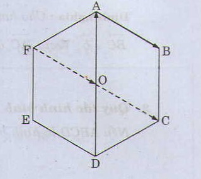
a) Các vec tơ cùng phương với vec tơ :
;
;
;
;
.
;
;
và
.
b) Các véc tơ bằng véc tơ :
;
;
.
SK
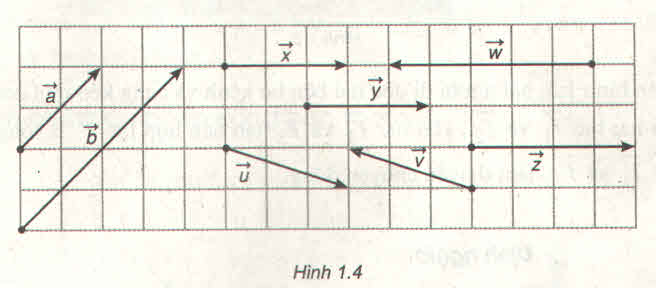
Trong hình 1.4 hãy chỉ ra các vectơ cùng phương, cùng hướng, ngược hướng và các vectơ bằng nhau :
Hướng dẫn giải
Thảo luận (1)
- Các vectơ cùng phương: và
;
,
,
và
;
và
.
- Các vectơ cùng hướng: và
;
,
,
- Các vectơ ngược hướng: và
;
và
;
và
;
và
.
- Các vectơ bằng nhau: =
.
SK
Cho ba vectơ overrightarrow{a},overrightarrow{b},overrightarrow{c} đều khác overrightarrow{0}. Các khẳng định sau đúng hay sai ?
a) Nếu hai vectơ overrightarrow{a},overrightarrow{b} cùng phương với overrightarrow{c} thì overrightarrow{a} và overrightarrow{b} cùng phương
b) Nếu overrightarrow{a}, overrightarrow{b} cùng ngược hướng với overrightarrow{c} thì overrightarrow{a} và overrightarrow{b} cùng hướng
Đọc tiếp
Cho ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) đều khác \(\overrightarrow{0}\). Các khẳng định sau đúng hay sai ?
a) Nếu hai vectơ \(\overrightarrow{a},\overrightarrow{b}\) cùng phương với \(\overrightarrow{c}\) thì \(\overrightarrow{a}\) và \(\overrightarrow{b}\) cùng phương
b) Nếu \(\overrightarrow{a}\), \(\overrightarrow{b}\) cùng ngược hướng với \(\overrightarrow{c}\) thì \(\overrightarrow{a}\) và \(\overrightarrow{b}\) cùng hướng
Hướng dẫn giải
Thảo luận (1)
a) Gọi theo thứ tự ∆1, ∆2, ∆3 là giá của các vectơ ,
,
cùng phương với
=> ∆1 //∆3 ( hoặc ∆1 = ∆3 ) (1)
cùng phương với
=> ∆2 // ∆3 ( hoặc ∆2 = ∆3 ) (2)
Từ (1), (2) suy ra ∆1 // ∆2 ( hoặc ∆1 = ∆2 ), theo định nghĩa hai vectơ ,
cùng phương.
Vậy câu a) đúng.
b) Câu này cũng đúng.
Trả lời bởi qwerty
SK
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \(\overrightarrow{AB}=\overrightarrow{DC}\) ?
Hướng dẫn giải
Thảo luận (1)
Ta chứng minh hai mệnh đề:
- Khi =
thì ABCD là hình bình hành.
Thật vậy, theo định nghĩa của vec tơ bằng nhau thì:
=
⇔
=
và và
cùng hướng.
và
cùng hướng =>
và
cùng phương, suy ra giá của chúng song song với nhau, hay AB // DC (1)
Ta lại có =
=> AB = DC (2)
Từ (1) và (2), theo dấu hiệu nhận biết hình bình hành, tứ giác ABCD có một cặp cạnh song song và bằng nhau nên nó là hình bình hành.
- Khi ABCD là hình bình hành thì =
Khi ABCD là hình bình hành thì AB // CD. Dễ thấy, từ đây ta suy ra hai vec tơ và
cùng hướng (3)
Mặt khác AB = CD => =
(4)
Từ (3) và (4) suy ra =
.
SK
Cho tứ giác ABCD. Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh \(\overrightarrow{NP}=\overrightarrow{MQ}\) và \(\overrightarrow{PQ}=\overrightarrow{NM}\) ?
Hướng dẫn giải
Thảo luận (1)
a)
Kẻ BD.
Trong tam giác ABD có MQ là đường trung bình nên MQ//BD và \(MQ=\dfrac{1}{2}BD\). (1)
Trong tam giác CBD có PN là đường trung bình nên PN//BD và \(NP=\dfrac{1}{2}BD\). (2)
Từ (1) và (2) suy ra: \(\overrightarrow{MQ}=\overrightarrow{NP}\).
Kẻ AC.
Trong tam giác ABC có MN là đường trung bình suy ra:
NM//CA và \(NM=\dfrac{1}{2}CA\). (3)
Trong tam giác DAC có PQ là đường trung bình nên:
PQ//AC và \(PQ=\dfrac{1}{2}CA\). (4)
Từ (3) và (4) suy ra: \(\overrightarrow{PQ}=\overrightarrow{NM}\).
a)
Trả lời bởi Bùi Thị VânDo \(\overrightarrow{AB}=\overrightarrow{DC}\) nên AB // DC và AB = DC .
Vì vậy tứ giác ABCD là là hình bình hành.
Từ đó suy ra: AD = BC và AD//BC nên \(\overrightarrow{AD}=\overrightarrow{BC}\).