vẽ đồ thị:
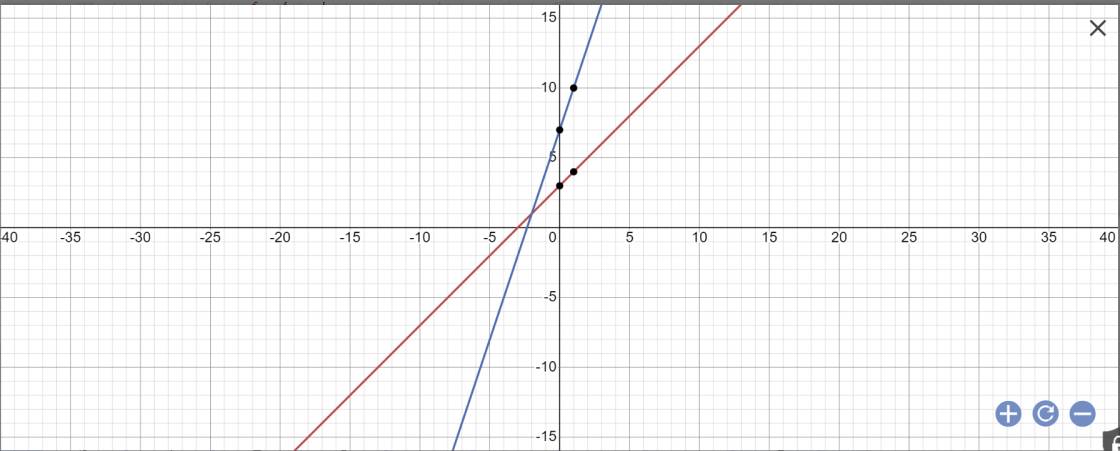
a: Phương trình hoành độ giao điểm là:
\(3x+7=x+3\)
=>3x-x=3-7
=>2x=-4
=>x=-2
Thay x=-2 vào y=x+3, ta được:
y=-2+3=1
Vậy: K(-2;1)
b: Sửa đề: I là trung điểm của đoạn thẳng nối bởi hai giao điểm của (d1) và (d2) với trục Oy
Tọa độ giao điểm của (d1) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=x+3=0+3=3\end{matrix}\right.\)
Tọa độ giao điểm của (d2) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=3x+7=3\cdot0+7=7\end{matrix}\right.\)
Tọa độ I là:
\(\left\{{}\begin{matrix}x=\dfrac{0+0}{2}=0\\y=\dfrac{3+7}{2}=\dfrac{10}{2}=5\end{matrix}\right.\)
Vậy: I(0;5)
Ta có: I(0;5); K(-2;1); O(0;0)
\(IK=\sqrt{\left(-2-0\right)^2+\left(1-5\right)^2}=\sqrt{2^2+4^2}=2\sqrt{5}\)
\(IO=\sqrt{\left(0-0\right)^2+\left(0-5\right)^2}=\sqrt{0^2+5^2}=5\)
\(KO=\sqrt{\left(0+2\right)^2+\left(0-1\right)^2}=\sqrt{2^2+1^2}=\sqrt{5}\)
Vì \(IK^2+KO^2=IO^2\)
nên ΔKIO vuông tại K
c: Vì ΔKIO vuông tại K
nên \(S_{IKO}=\dfrac{1}{2}\cdot IK\cdot KO=\dfrac{1}{2}\cdot2\sqrt{5}\cdot\sqrt{5}=5\)


