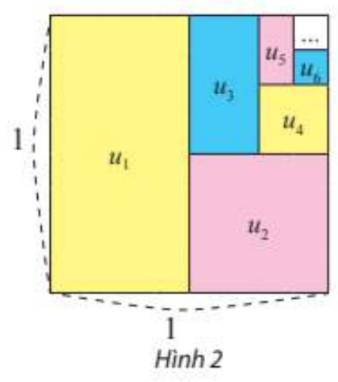
Từ một hình vuông có cạnh bằng 1, tô màu một nửa hình vuông, rồi tô màu một nửa hình còn lại và cứ tiếp tục như vậy (xem Hình 2).
a) Xác định diện tích \({u_k}\) của phần hình được tô màu lần thứ \(k\left( {k = 1,2,3,...} \right)\).
b) Tính tổng diện tính \({S_n}\) của phần hình được tô màu sau lần tô thứ \(n\left( {n = 1,2,3,...} \right)\).
c) Tìm giới hạn \(\lim {S_n}\) và so sánh giới hạn này với diện tích hình vuông ban đầu.
a) Theo đề bài, ta thấy \(\left( {{u_k}} \right)\) là cấp số nhân với số hạng đầu \({u_1} = \frac{1}{2}\), công bội \(q = \frac{1}{2}\).
Vậy \({u_k} = {u_1}.{q^{k - 1}} = \frac{1}{2}.{\left( {\frac{1}{2}} \right)^{k - 1}} = {\left( {\frac{1}{2}} \right)^k} = \frac{1}{{{2^k}}}\).
b) \(\left( {{u_n}} \right)\) là cấp số nhân với số hạng đầu \({u_1} = \frac{1}{2}\), công bội \(q = \frac{1}{2}\).
Vậy \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}} = \frac{1}{2}.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = \frac{1}{2}.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{\frac{1}{2}}} = 1 - {\left( {\frac{1}{2}} \right)^n}\).
c) \(\lim {S_n} = \lim \left( {1 - {{\left( {\frac{1}{2}} \right)}^n}} \right) = \lim 1 - \lim {\left( {\frac{1}{2}} \right)^n}\).
\(\lim 1 = 1\) vì 1 là hằng số.
\(\left| {\frac{1}{2}} \right| = \frac{1}{2} < 1\) nên \(\lim {\left( {\frac{1}{2}} \right)^n} = 0\)
Vậy \(\lim {S_n} = \lim 1 - \lim {\left( {\frac{1}{2}} \right)^n} = 1 - 0 = 1\)
Giới hạn này bằng diện tích của hình vuông ban đầu.