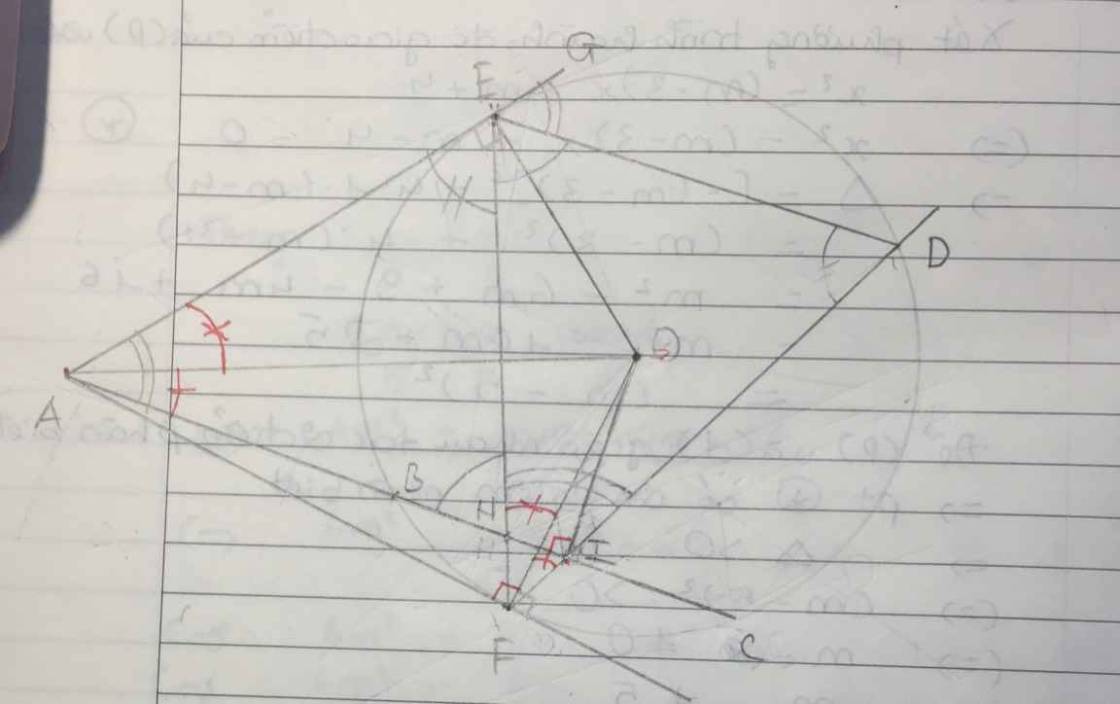
a: góc OBA+góc OCA=180 độ
=>OBAC nội tiếp
Xét(O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>H là trung điểm của BC
b: Xét ΔBHE và ΔDHC có
góc BHE=góc DHC
góc HBE=góc HDC
=>ΔBHE đồng dạng với ΔDHC
=>BE/CD=HE/HC
Xet ΔCHE và ΔDHB có
góc CHE=góc DHB
góc HCE=góc HDB
=>ΔCHE đồng dạng với ΔDHB
=>CE/BD=HE/HB
=>BE/CD=CE/BD
=>BD*BE=CD*CE