\(\dfrac{\sqrt{3}}{2}< 1;\dfrac{\sqrt[3]{26}}{3}< 1;\pi>1;\dfrac{\sqrt{15}}{4}< 1\)
Hàm số đồng biến là: \(log_{\pi}x\)
Hàm số nghịch biến là: \(\left(\dfrac{\sqrt{3}}{2}\right)^x;\left(\dfrac{\sqrt[3]{26}}{3}\right)^x;log_{\dfrac{\sqrt{15}}{4}}x\)
\(\dfrac{\sqrt{3}}{2}< 1;\dfrac{\sqrt[3]{26}}{3}< 1;\pi>1;\dfrac{\sqrt{15}}{4}< 1\)
Hàm số đồng biến là: \(log_{\pi}x\)
Hàm số nghịch biến là: \(\left(\dfrac{\sqrt{3}}{2}\right)^x;\left(\dfrac{\sqrt[3]{26}}{3}\right)^x;log_{\dfrac{\sqrt{15}}{4}}x\)
Tìm tập xác định của các hàm số:
a) \(y = 12{}^x\)
b) \(y = {\log _5}(2x - 3)\)
c) \(y = {\log _{\frac{1}{5}}}\left( { - {x^2} + 4} \right)\)
Luyện tập – Vận dụng 4
Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {\log _{\frac{1}{3}}}x\)
Luyện tập – Vận dụng 2
Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\)
Lập bảng biến thiên và vẽ đồ thị hàm số:
a) \(y = {4^x}\)
b) \(y = {\log _{\frac{1}{4}}}x\)
Cho hàm số lôgarit \(y = {\log _{\frac{1}{2}}}x\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
b, Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a.
Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_{\frac{1}{2}}}x} \right)\) với \(x \in (0; + \infty )\) và nối lại ta được đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\) như hình bên.
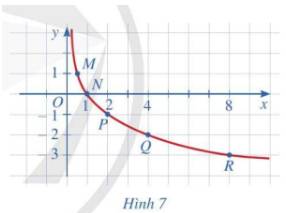
c, Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\) với trục hoành và vị trí của đồ thị hàm số đó với trục tung.
d, Quan sát đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\), nêu nhận xét về:
\(\mathop {\lim }\limits_{x \to {0^ + }} ({\log _{\frac{1}{2}}}x)\,;\mathop {\,\,\mathop {\lim }\limits_{x \to + \infty } ({{\log }_{\frac{1}{2}}}x)}\limits_{} \)Sự biến thiên của hàm số \(y = {\log _{\frac{1}{2}}}x\) và lập bảng biến thiên của hàm số đó.Cho hàm số lôgarit \(y = {\log _2}x\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
b, Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a.
Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_2}x} \right)\) với \(x \in (0; + \infty )\) và nối lại ta được đồ thị hàm số \(y = {\log _2}x\) như hình bên.
c, Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {\log _2}x\) với trục hoành và vị trí của đồ thị hàm số đó với trục tung.
d, Quan sát đồ thị hàm số \(y = {\log _2}x\), nêu nhận xét về:
\(\mathop {\mathop {\lim }\limits_{x \to {0^ + }} ({{\log }_2}x)}\limits_{} \,;\mathop {\,\,\mathop {\lim }\limits_{x \to + \infty } ({{\log }_2}x)}\limits_{} \)Sự biến thiên của hàm số \(y = {\log _2}x\) và lập bảng biến thiên của hàm số đóHoạt động 3
Cho hàm số mũ \(y = {\left( {\frac{1}{2}} \right)^x}\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
b, Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm trong bảng giá trị ở câu a.
Bằng cách tương tự, lấy nhiều điểm \(\left( {x;{{\left( {\frac{1}{2}} \right)}^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) (Hình 2)

c, Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) với trục tung và vị trí của đồ thị hàm số đó so với trục hoành.
d, Quan sát đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\), nêu nhận xét về:
\(\mathop {\lim {{\left( {\frac{1}{2}} \right)}^x}}\limits_{x \to + \infty } ;\,\mathop {\lim {{\left( {\frac{1}{2}} \right)}^x}}\limits_{x \to - \infty } \)Sự biến thiên của hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) và lập bảng biến thiên của hàm số đó.
Cho hàm số mũ \(y = {2^x}\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm trong bảng giá trị ở câu a.
Bằng cách tương tự, lấy nhiều điểm \(\left( {x;{2^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị hàm số \(y = {2^x}\) (Hình 1)
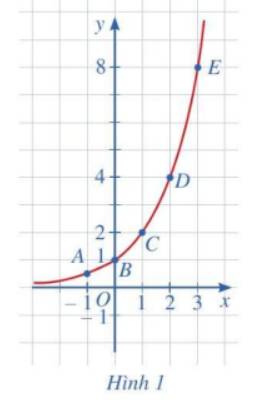
c) Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {2^x}\) với trục tung và vị trí của đồ thị hàm số đó so với trục hoành.
d) Quan sát đồ thị hàm số \(y = {2^x}\), nêu nhận xét về:
\(\mathop {\lim {2^x}}\limits_{x \to + \infty } ;\,\mathop {\lim {2^x}}\limits_{x \to - \infty } \)Sự biến thiên của hàm số \(y = {2^x}\) và lập bảng biến thiên của hàm số đó.Ta coi năm lấy làm mốc để tính dân số của một vùng (hoặc một quốc gia) là năm 0. Khi đó, dân số của quốc gia đó ở năm thứ t là hàm số theo biến t được cho bởi công thức \(S = A.{e^{r.t}}\). Trong đó A là dân số của vùng (hoặc quốc gia) đó ở năm O và r là tỉ lệ tăng dân số hàng năm. Biết rằng dân số Việt Nam năm 2021 ước tính là 98 564 407 người và tỉ lệ tăng dân số là 0,93%/năm. Giả sử tỉ lệ tăng dân số hàng năm là như nhau tính từ năm 2021, nêu dự đoán dân số Việt Nam năm 2030 (làm tròn kết quả đến hàng đơn vị).