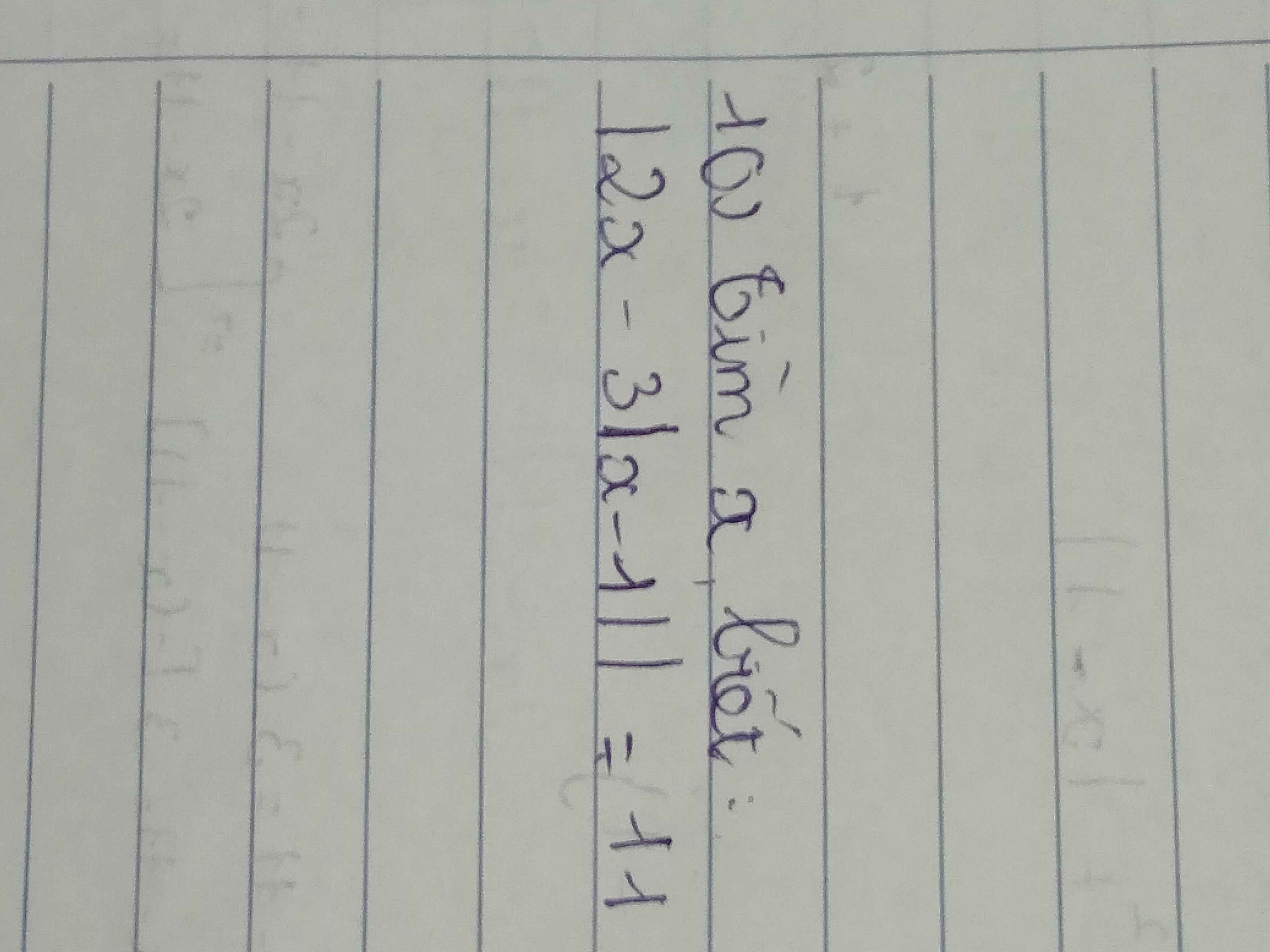\(3^x+1=\frac{1}{3}\)
=> \(3^x=\frac{1}{3}-1\)
=> \(3^x=-\frac{2}{3}\)
Vì \(3^x>\) hoặc \(=0\) \(\forall x.\)
=> \(3^x\ne-\frac{2}{3}\)
Vậy không tồn tại giá trị nào của \(x\) thỏa mãn yêu cầu đề bài.
Chúc bạn học tốt!
Đúng 0
Bình luận (0)
\(3^x+1=\frac{1}{3}\)
\(\Leftrightarrow3^x=\frac{1}{3}-1\)
\(\Leftrightarrow3^x=\frac{-2}{3}\)
\(\Leftrightarrow x\in\varnothing\)
Đúng 0
Bình luận (0)
