Em xin lỗi, p.số cuối ở số 1 ở ngoài căn ạ, em đánh lộn:
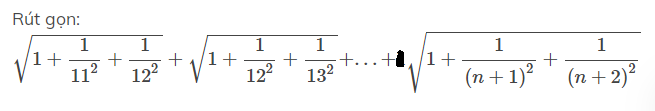
Áp dụng hằng đẳng thức: \(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}=\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2\) nếu \(a+b+c=0\) là ra
ĐK: \(n>0\)
Ta có: \(\left(1+\dfrac{1}{n}-\dfrac{1}{n+1}\right)^2\)
\(=1+\dfrac{1}{n^2}+\dfrac{1}{\left(n+1\right)^2}+2\left(\dfrac{1}{n}-\dfrac{1}{n+1}-\dfrac{1}{n\left(n+1\right)}\right)\)
\(=1+\dfrac{1}{n^2}+\dfrac{1}{\left(n+1\right)^2}+2.\dfrac{n+1-n-1}{n\left(n+1\right)}\)
\(=1+\dfrac{1}{n^2}+\dfrac{1}{\left(n+1\right)^2}+0=1+\dfrac{1}{n^2}+\dfrac{1}{\left(n+1\right)^2}\)
Áp dụng:
\(\sqrt{1+\dfrac{1}{11^2}+\dfrac{1}{12^2}}+\sqrt{1+\dfrac{1}{12^2}+\dfrac{1}{13^2}}+...+\sqrt{1+\dfrac{1}{\left(n+1\right)^2}+\dfrac{1}{\left(n+2\right)^2}}\)
\(=\sqrt{\left(1+\dfrac{1}{11}-\dfrac{1}{12}\right)^2}+\sqrt{\left(1+\dfrac{1}{12}-\dfrac{1}{13}\right)^2}+...+\sqrt{\left(1+\dfrac{1}{n+1}-\dfrac{1}{n+2}\right)^2}\)
\(=\left|1+\dfrac{1}{11}-\dfrac{1}{12}\right|+\left|1+\dfrac{1}{12}-\dfrac{1}{13}\right|+...+\left|1+\dfrac{1}{n+1}-\dfrac{1}{n+2}\right|\)
\(=1+\dfrac{1}{11}-\dfrac{1}{12}+1+\dfrac{1}{12}-\dfrac{1}{13}+...+1+\dfrac{1}{n+1}-\dfrac{1}{n+2}\)
\(=\left(n-9\right)+\dfrac{1}{11}-\dfrac{1}{n+2}=n-\dfrac{1}{n+2}-\dfrac{98}{11}\)



