a, Điều kiện: x > 0
\(log_3\left(x\right)< 2\\ \Rightarrow0< x< 9\)
b, Điều kiện: x > 5
\(log_{\dfrac{1}{4}}\left(x-5\right)\ge-2\\ \Rightarrow x-5\le16\\ \Leftrightarrow5< x\le21\)
a, Điều kiện: x > 0
\(log_3\left(x\right)< 2\\ \Rightarrow0< x< 9\)
b, Điều kiện: x > 5
\(log_{\dfrac{1}{4}}\left(x-5\right)\ge-2\\ \Rightarrow x-5\le16\\ \Leftrightarrow5< x\le21\)
Đề bài
Giải mỗi bất phương trình sau:
a) \({3^x} > \frac{1}{{243}}\)
b) \({\left( {\frac{2}{3}} \right)^{3x - 7}} \le \frac{3}{2}\)
c) \({4^{x + 3}} \ge {32^x}\)
d) \(\log (x - 1) < 0\)
e) \({\log _{\frac{1}{5}}}(2x - 1) \ge {\log _{\frac{1}{5}}}(x + 3)\)
f) \(\ln (x + 3) \ge \ln (2x - 8)\)
Luyện tập – Vận dụng 6
Giải mỗi bất phương trình sau:
a) \({7^{x + 3}} < 343\)
b) \({\left( {\frac{1}{4}} \right)^x} \ge 3\)
Giải mỗi phương trình sau:
a) \({\log _5}\left( {2x - 4} \right) + {\log _{\frac{1}{5}}}\left( {x - 1} \right) = 0\)
b) \({\log _2}x + {\log _4}x = 3\)
Đề bài
Giải mỗi phương trình sau:
a) \({\left( {0,3} \right)^{x - 3}} = 1\)
b) \({5^{3x - 2}} = 25\)
c) \({9^{x - 2}} = {243^{x + 1}}\)
d) \({\log _{\frac{1}{x}}}(x + 1) = - 3\)
e) \({\log _5}(3x - 5) = {\log _5}(2x + 1)\)
f) \({\log _{\frac{1}{7}}}(x + 9) = {\log _{\frac{1}{7}}}(2x - 1)\)
a) Vẽ đồ thị hàm số \(y = {\log _4}x\) và đường thẳng y = 5
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình \({\log _4}x = 5\)
Luyện tập – Vận dụng 7
Cho hai ví dụ về bất phương trình logarit cơ bản
Luyện tập – Vận dụng 5
Cho hai ví dụ về bất phương trình mũ cơ bản
Giải mỗi phương trình sau:
a) \({9^{16 - x}} = {27^{x + 4}}\)
b) \({16^{x - 2}} = 0,{25.2^{ - x + 4}}\)
Hoạt động 6
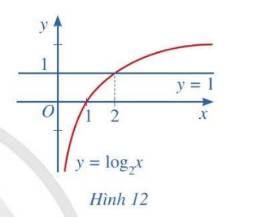
Quan sát Hình 12 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số lôgarit \(y = {\log _2}x\). Từ đó, hãy tìm x sao cho \({\log _2}x > 1\)