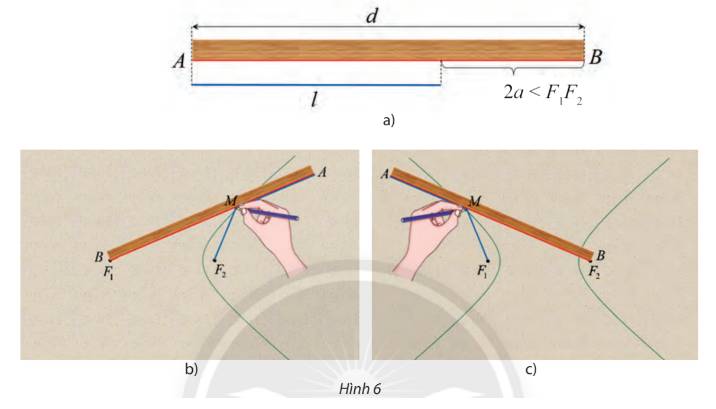
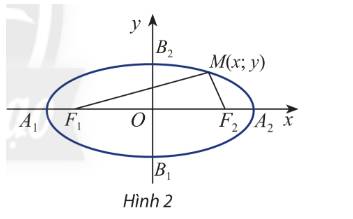
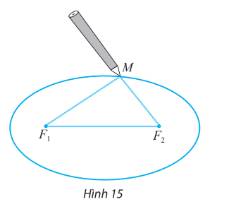
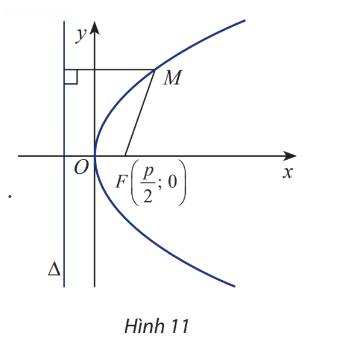
Lấy một tấm bìa, ghim hai cái đinh lên đó tại hai điểm \({F_1}\) và \({F_2}\). Lấy một vòng dây kín không đàn hồi có độ dài lớn hơn hai lần đoạn \({F_1}{F_2}\). Quàng vòng dây đó qua hai chiếc đinh và kéo căng tại một điểm M nào đó. Tựa đầu bút chì vào trong vòng dây tại điểm M rồi di chuyển sao cho dây luôn luôn căng. Đầu bút chì vạch lên tấm bìa một đường mà người ta gọi là đường elip.
Cho biết 2c là khoảng cách \({F_1}{F_2}\) và \(2a + 2c\) là độ dài của vòng dây.
Tính tổng hai khoảng cách \({F_1}M\) và \({F_2}M\)
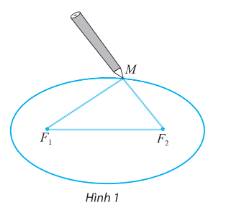
Ta có chiều dài vòng dây là:
\(M{F_1} + {F_1}{F_2} + {F_2}M = 2a + 2c \Rightarrow M{F_1} + {F_2}M = 2a + 2c - {F_1}{F_2} = 2a\)
Vậy tổng khoảng cách \({F_1}M\) và \({F_2}M\) là 2a