\(a,=\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{7}\left(\sqrt{5}-\sqrt{2}\right)}=\dfrac{\sqrt{21}}{7}\\ b,=\dfrac{\sqrt{5}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{4}\left(\sqrt{3}+\sqrt{2}\right)}=\dfrac{\sqrt{5}}{2}\\ c,=\dfrac{\sqrt{x}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)}=\dfrac{\sqrt{xy}}{y}\\ d,=\dfrac{\left(\sqrt{3}-\sqrt{2}\right)\left(2\sqrt{5}-\sqrt{3}\right)}{\left(2\sqrt{5}-\sqrt{3}\right)\left(1-\sqrt{2}\right)}=\dfrac{\sqrt{3}-\sqrt{2}}{1-\sqrt{2}}\\ =\left(\sqrt{2}-\sqrt{3}\right)\left(\sqrt{2}+1\right)=2+\sqrt{2}-\sqrt{6}+\sqrt{3}\)
c: \(=7-3\cdot2+3\)
=10-9
=1





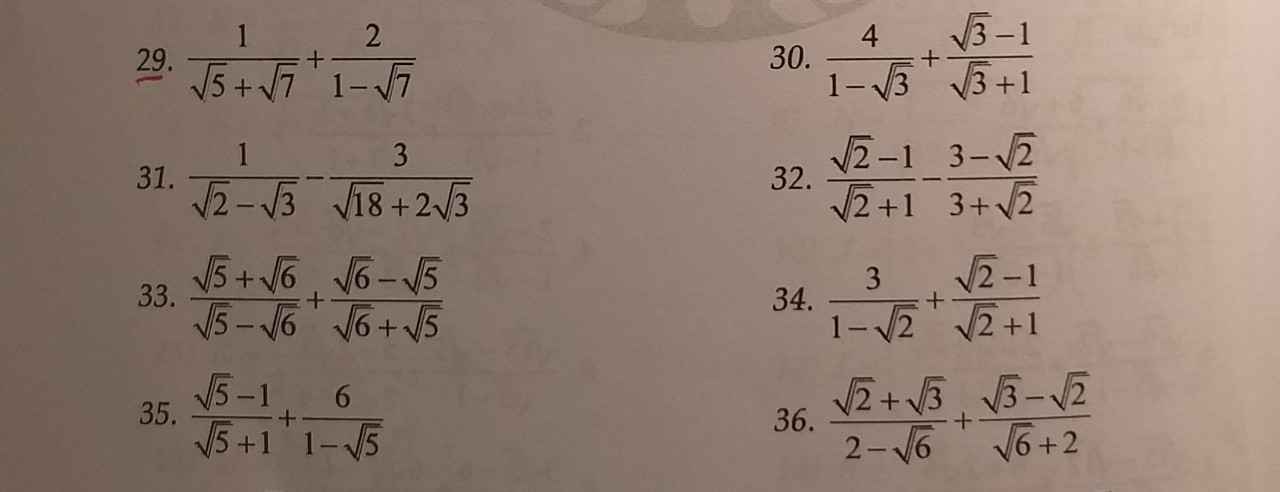






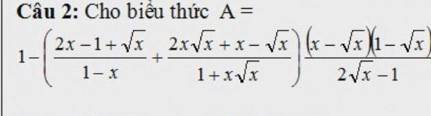
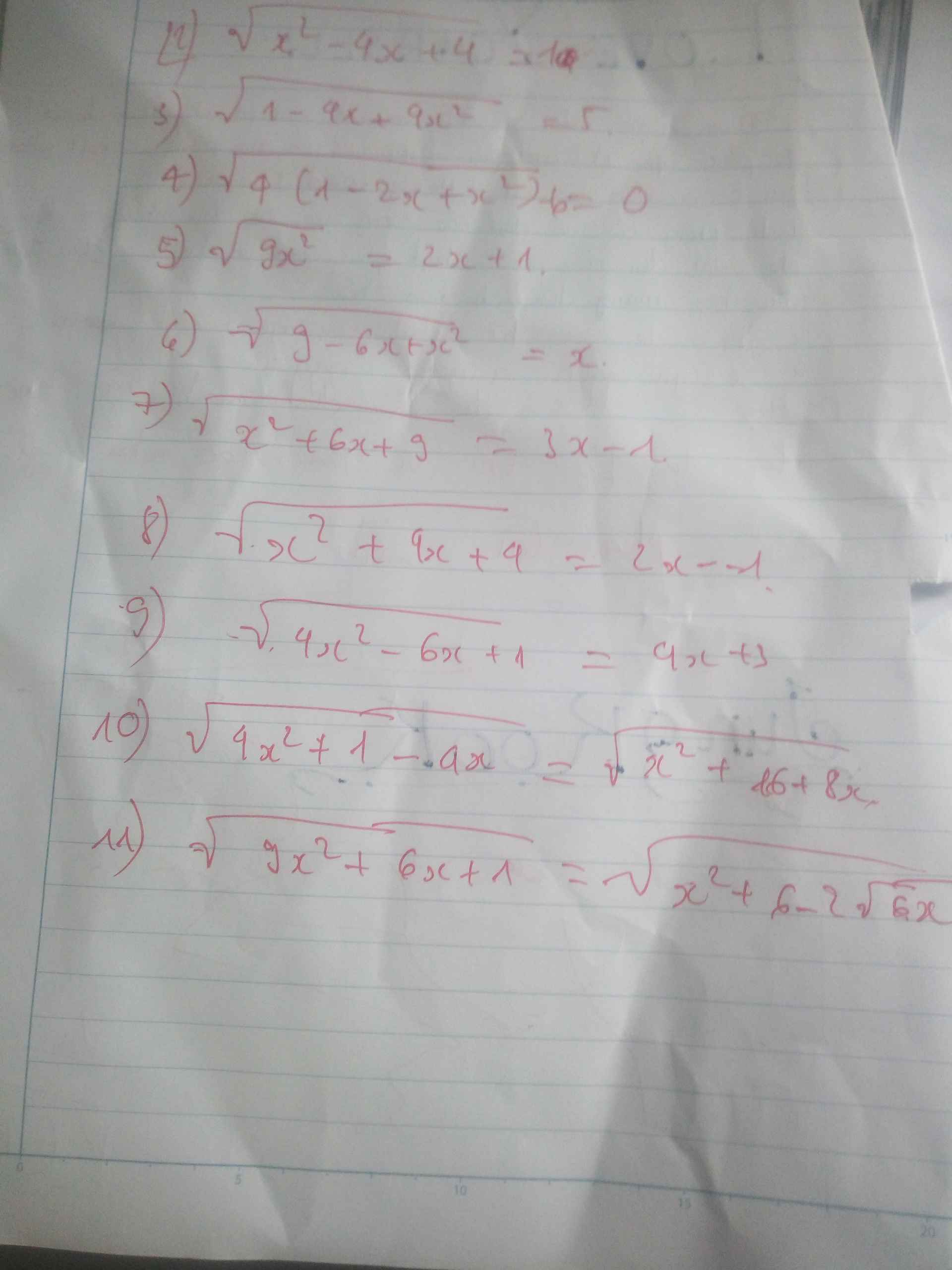
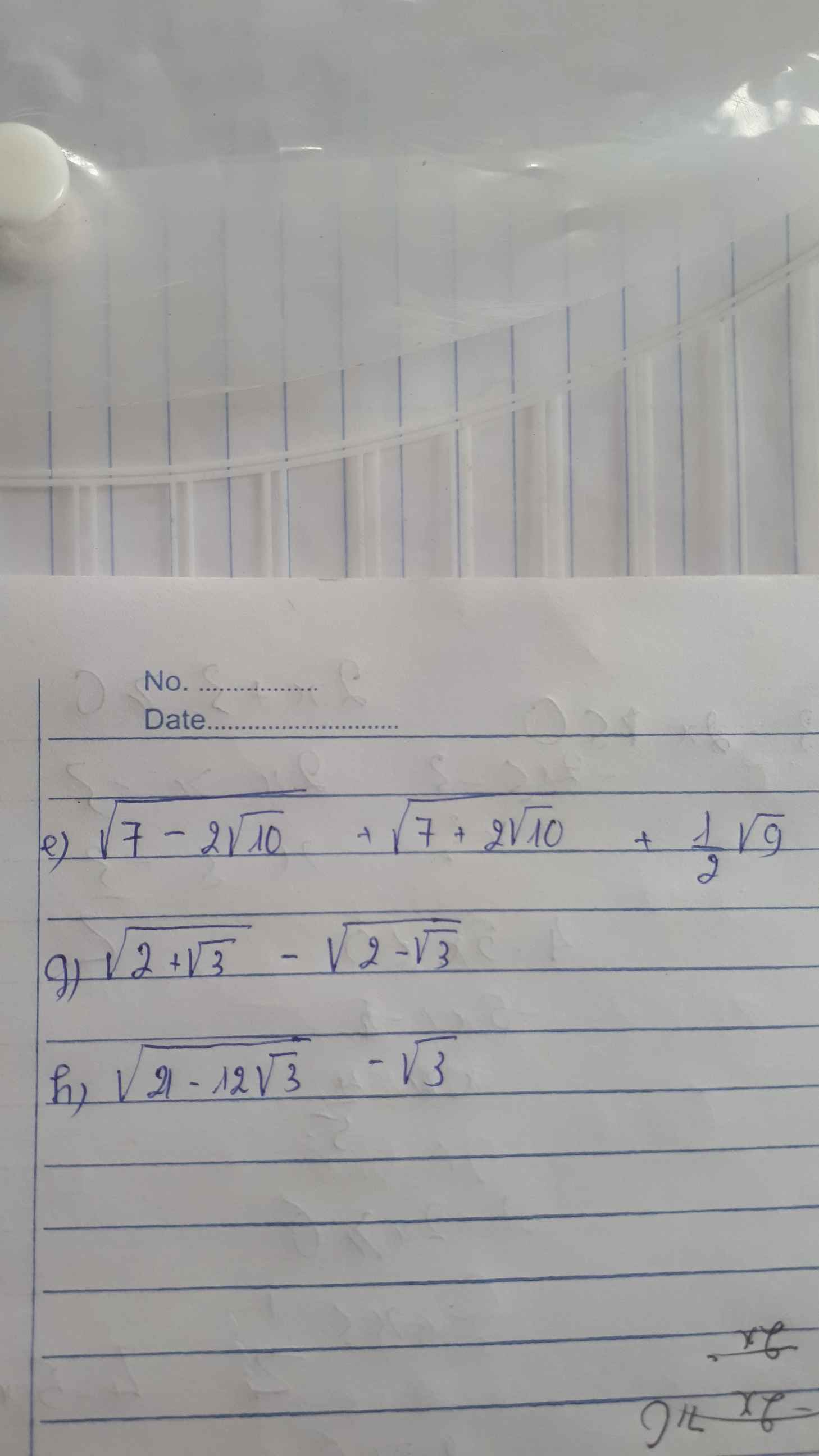

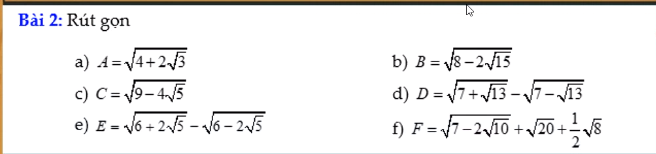 giúp mik với cả 2 bài nha
giúp mik với cả 2 bài nha