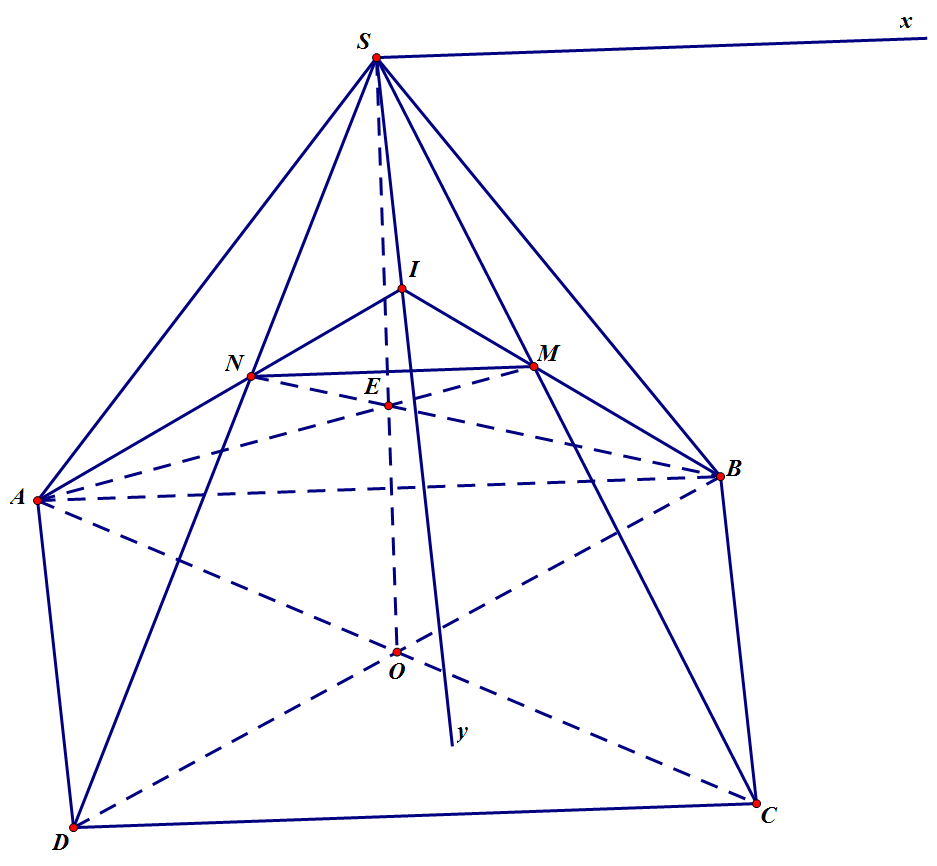
a, (SAB) và (SCD) có chung điểm S. Mà AB \(\subset\) (SAB) ; CD \(\subset\) (SCD) và ta có AB // CD
⇒ (SAB) \(\cap\) (SCD) = Sx. Với Sx là đường thẳng đi qua S và song song với AB và CD
b, M ∈ SC nên M ∈ (SAC)
Trong (ABCD) gọi O = AC \(\cap\) BD ⇒ O là trung điểm của AC và BD
Trong (SAC) gọi E = AM \(\cap\) SO
Do N = SD \(\cap\) (BMN) nên N nằm trên giao tuyến của (SBD) và (BMN)
⇒ N nằm trên BE do BE = (SBD) \(\cap\) (BMN)
⇒ N = BE \(\cap\) SD
Ta có 3 mặt phẳng : (SAB); (SCD) ; (BMN) phân biệt và
(SAB) \(\cap\) (SCD) = Sx
(SAB) \(\cap\) (BMN) = AB
(BMN) \(\cap\) (SCD) = MN. Mà Sx // AB
=> AB // Sx // MN
⇒ Tứ giác ABMN là hình thang
c, Do I = AN \(\cap\) BM. Mà AN \(\subset\) (SAD) và BM \(\subset\) (SBC)
⇒ I nằm trên giao tuyến của (SAD) và (SBC)
=> I nằm trên đường thẳng Sy đi qua S và Sy // AD // BC











