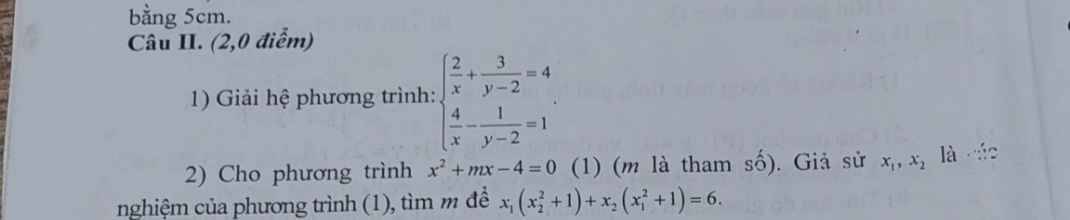1.
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0\\y\ne2\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=u\\\dfrac{1}{y-2}=v\end{matrix}\right.\) ta được:
\(\left\{{}\begin{matrix}2u+3v=4\\4u-v=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2u+3v=4\\v=4u-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2u+3\left(4u-1\right)=4\\v=4u-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}14u=7\\v=4u-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{1}{2}\\v=4.\dfrac{1}{2}-1=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{2}\\\dfrac{1}{y-2}=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\y-2=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)
2.
\(\Delta=m^2+16>0;\forall m\Rightarrow\) pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=-4\end{matrix}\right.\)
\(x_1\left(x^2_2+1\right)+x_2\left(x_1^2+1\right)=6\)
\(\Leftrightarrow x_1x_2\left(x_1+x_2\right)+x_1+x_2=6\)
\(\Leftrightarrow4m-m=6\)
\(\Rightarrow m=2\)
Ý 1:
\(Đặt:\left\{{}\begin{matrix}\dfrac{1}{x}=a\left(x\ne0\right)\\\dfrac{1}{y-2}=b\left(y\ne2\right)\end{matrix}\right.\\ \left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{3}{y-2}=4\\\dfrac{4}{x}-\dfrac{1}{y-2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+3b=4\\4a-b=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}4a+6b=8\\4a-b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7b=7\\4a-b=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=1\\a=\dfrac{1}{2}\end{matrix}\right.\left(TM\right)\\ \Rightarrow\left\{{}\begin{matrix}x=1\\y=4\end{matrix}\right.\)
Vậy hpt có cặp nghiệp (x;y)= (1;4)