ướng dẫn:
Vì L và M đối xứng qua đường thẳng xy. Nên đường thẳng xy là trung trực của ML
I ∈ xt => IM = IL

Nên IM + IN = IL + IN
+ Nếu I là giao điểm của NL và xy thì IL + IN = LN
+ Nếu I không là giao điểm của NL và xy thì ba điểm I, N, L không thẳng hàng
=> IL + IN > LN
Vậy với mọi vị trí của I trên xy thì IL + IN ≥ LN
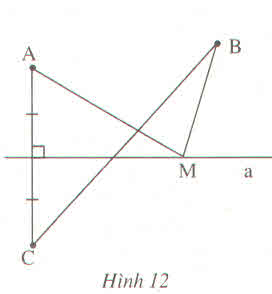
48. Hai điểm M và N cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng xy.
Lấy điểm L đối xứng với M qua xy. Gọi I là một điểm của xy. Hãy so sánh IM + IN với LN.
Hướng dẫn:
Vì L và M đối xứng qua đường thẳng xy. Nên đường thẳng xy là trung trực của ML
I ∈ xt => IM = IL

Nên IM + IN = IL + IN
+ Nếu I là giao điểm của NL và xy thì IL + IN = LN
+ Nếu I không là giao điểm của NL và xy thì ba điểm I, N, L không thẳng hàng
=> IL + IN > LN
Vậy với mọi vị trí của I trên xy thì IL + IN ≥ LN
Vì L đối xứng với M nên xy là đường trung trực của đoạn thẳng ML.
Mà \(I\in xy\Rightarrow IM=IL\)(Định lý 1)
Xét \(\Delta ILN\)có: IL + IN > LN (bất đẳng thức tam giác)
Mà: IM = IL (cmt) \(\Rightarrow IM+IN>LN\)
Vậy: IM + IN > LN